Question

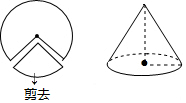
2．如圖，從半徑為9cm的圓形紙片中剪去一個扇形，使剪去的扇形的弧長為圓周長的$\frac{1}{3}$，將留下的扇形紙片圍成一個圓錐（接縫處不重疊），則這個圓錐的高為（　　）

• A． 6cm
• B． 3$\sqrt{5}$cm
• C． 8cm
• D． 5$\sqrt{3}$cm

Answer 1

分析 首先求得圓錐的底面半徑的長，然后根據勾股定理求得高即可．

解答 解：∵從半徑為9cm的圓形紙片剪去$\frac{1}{3}$圓周的一個扇形，
∴留下的扇形圓心角為：360°×$\frac{2}{3}$=240°，
∴留下的扇形的弧長=$\frac{240π•9}{180}$=12π，
根據底面圓的周長等于扇形弧長，
∴圓錐的底面半徑r=$\frac{12π}{2π}$=6cm，
所以圓錐的高=$\sqrt{{9}^{2}-{6}^{2}}$=3$\sqrt{5}$cm．
故選B．

點評 此題主要考查了圓錐的性質，要知道（1）圓錐的高，底面半徑，母線構成直角三角形，（2）此扇形的弧長等于圓錐底面周長，扇形的半徑等于圓錐的母線長．解此類題目要根據所構成的直角三角形的勾股定理作為等量關系求解．