
分析 (1)先寫出每個數產生的原始數,相加得到它們的終止數.
(2)根據各個原始數的和與終止數相等,得到原始數各個數位的數字和,然后寫出滿足條件的所有原始數.
解答 解:(1)有題意可得原始數243可產生234,324,342,432,423這六個數相加為243+234+324+342+432+423=1998.
原式數537可產生573,357,375,753,735這六個數相加為數537+573+357+375+753+735=3330.
(2)原始數$\overline{4ab}$可產生的數有$\overline{4ba}$,$\overline{a4b}$,$\overline{ab4}$,$\overline{b4a}$,$\overline{ba4}$,
終止數=400+10a+b+400+10b+a+100a+40+b+100a+10b+4+100b+40+a+100b+10a+4=888+222a+222b,
原始數$\overline{12a}$可產生的數有$\overline{1a2}$,$\overline{a21}$,$\overline{a12}$,$\overline{21a}$,$\overline{2a1}$終止數=100+20+a+100+10a+2+100a+20+1+100a+10+2+200+10+a+200+10a+1=222a+666,
∵原始數$\overline{4ab}$的終止數是原始數$\overline{12a}$的終止數的3倍,
∴(888+222a+222b)÷(222a+666)=3,
∴2a+5=b,
∵0<a≤9,0<b≤9,且a、b整數,
∴$\left\{\begin{array}{l}{a=1}\\{b=7}\end{array}\right.$,$\left\{\begin{array}{l}{a=2}\\{b=9}\end{array}\right.$,
∴這兩個原式數為417,121或者429,122.
點評 本題考查了寫原始數,算終止數,屬于新定義類問題.掌握原式數的得到規律,找到各個數位間的數字關系是解決本題的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系xOy中,一次函數y=ax+b的圖象與反比例函數y=$\frac{k}{x}$的圖象相交于點A(-4,-2),B(m,4),與y軸相交于點C.
如圖,在平面直角坐標系xOy中,一次函數y=ax+b的圖象與反比例函數y=$\frac{k}{x}$的圖象相交于點A(-4,-2),B(m,4),與y軸相交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 運算程序 | 例如 | 按左側的形式完成你的舉例 |
| ①從1~9這9個數字中,任意選擇3個不同的數字 | 3、2、5 | 1、2、3 |
| ②由這三個數字組成6個不同的三位數(個位數字、十位數字、百位數字互相不重復) | 325、352、253、235、523、532 | 123、132、213、231、312、321 |
| ③將②中這6個三位數相加 | 325+352+253+235+523+532=a= 2220 | 1332 |
| ④用③所得的和除以這三個數字的和,得結果 | a÷(3+2+5)= 222 | 222 |
| 運算程序 | 運算過程 |
| ①從1~9這9個數字中,任意選擇3個不同的數字 | a、b、c,且a≠b≠c |
| ②由這三個數字組成6個不同的三位數(個位數字、十位數字、百位數字互相不重復) | |
| ③將②中這6個三位數相加 | |
| ④用③所得的和除以這三個數字的和,得結果 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
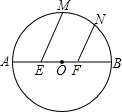 如圖,AB為⊙O的直徑,E、F為AB的三等分點,M、N為$\widehat{AB}$上兩點,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,則直徑AB的長為6.
如圖,AB為⊙O的直徑,E、F為AB的三等分點,M、N為$\widehat{AB}$上兩點,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,則直徑AB的長為6.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -2與$\sqrt{{{(-2)}^2}}$ | B. | -2與$\root{3}{-8}$ | C. | -2與$-\frac{1}{2}$ | D. | 2與|-2| |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com