
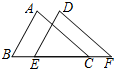
 已知:如圖,E、C是BF上兩點,且AB∥DE,BE=FC,∠A=∠D.求證:AC=DF.
已知:如圖,E、C是BF上兩點,且AB∥DE,BE=FC,∠A=∠D.求證:AC=DF. 分析 先根據平行線的性質得∠B=∠DEF,再由BE=FC得到BC=EF,則可根據“AAS”判斷△ABC≌△DEF,然后根據全等三角形的性質即可得到AC=DF.
解答 證明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=FC,
∴BE+EC=EC+CF,即BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{A=∠D}\\{∠B=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF,
∴AC=DF.
點評 本題考查了全等三角形的判定與性質:全等三角形的判定是結合全等三角形的性質證明線段和角相等的重要工具.在應用全等三角形的判定時,要注意三角形間的公共邊和公共角,必要時添加適當輔助線構造三角形;在應用全等三角形的性質時主要是得到對應角相等或對應線段相等.


科目:初中數學 來源: 題型:選擇題
| A. | 任意擲一枚均勻的硬幣,正面朝上 | B. | 籃球運動員投籃,投進籃筐 | ||
| C. | 一個星期有七天 | D. | 打開電視機,正在播放新聞 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
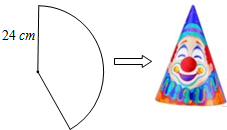 小洋用一張半徑為24cm的扇形紙板做一個如圖所示的圓錐形小丑帽子側面(接縫忽略不計),如果做成的圓錐形小丑帽子的底面半徑為10cm,那么這張扇形紙板的面積是( )
小洋用一張半徑為24cm的扇形紙板做一個如圖所示的圓錐形小丑帽子側面(接縫忽略不計),如果做成的圓錐形小丑帽子的底面半徑為10cm,那么這張扇形紙板的面積是( )| A. | 120πcm2 | B. | 240πcm2 | C. | 260πcm2 | D. | 480πcm2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com