
分析 (1)如圖1中,作DF⊥BC于F,AN⊥BC于N,連接BD.首先證明點B、D、C在以A為圓心的圓上,推出△BDF是等腰直角三角形,再證明tan∠ABC=tan∠ACB=tan∠FDE=tan∠EAN=$\frac{1}{2}$,設EN=a,則AN=2a,CN=BN=4a,推出BF=DF=2a,EF=a,EC=5a,再根據AC=2$\sqrt{5}$a=2$\sqrt{2}$,求出a即可解決問題.
(2)如圖2中,連接DF,延長AF交BD于M.首先證明△BFD是等腰直角三角形,再證明△AMD≌△CGA,推出AG=DM=BM=FM,CG=AM,由△BFD是等腰直角三角形,FM⊥BD,推出∠BFM=∠AFN=45°,推出$\sqrt{2}$BF=$\sqrt{2}$AN=AF,由此即可證明.
(3)如圖3中,作AM⊥BC于M,連接DF.FA的延長線交BD于N.首先證明BD=$\sqrt{2}$BF,由sin∠ABC=$\frac{1}{2}$,推出∠ABC=∠ACB=∠EAM=30°,設EM=m則AE=2m,EC=4m,AM=FM=$\sqrt{3}$m,CF=CM=FM=3m-$\sqrt{3}$m,FG=$\frac{3m-\sqrt{3}m}{\sqrt{2}}$,由此即可解決問題.
解答 (1)解:如圖1中,作DF⊥BC于F,AN⊥BC于N,連接BD.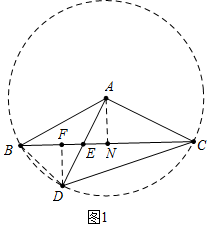
∵AB=AD=AC,
∴點B、D、C在以A為圓心的圓上,
∵DA⊥AC,
∴∠DAC=90°,
∴∠DBC=$\frac{1}{2}$∠DAC=45°,
∵∠DFB=90°,
∴△BDF是等腰直角三角形,
∴DF=BF,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACE+∠AEC=90°,∠FDE+∠FED=90°,∠FED=∠AED,
∴∠FDE=∠ACB=∠ABC,
∵∠EAN+∠AEC=90°,∠ACB+∠AEC=90°,
∴∠EAN=∠ACB,
∴tan∠ABC=tan∠ACB=tan∠FDE=tan∠EAN=$\frac{1}{2}$,設EN=a,則AN=2a,CN=BN=4a,
∴BE=3a,
∵BF=DF=2EF,
∴BF=DF=2a,EF=a,CE=5a,
在Rt△ADC中,∵CD=4,
∴AD=AC=2$\sqrt{2}$,
又∵AC=$\sqrt{A{N}^{2}+N{C}^{2}}$=$\sqrt{(2a)^{2}+(4a)^{2}}$=2$\sqrt{5}$a,
∴2$\sqrt{5}$a=2$\sqrt{2}$,
∴a=$\frac{\sqrt{10}}{5}$,
∴EC=5a=$\sqrt{10}$.
(2)證明:如圖2中,連接DF,延長AF交BD于M.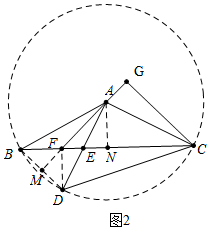
∵AF平分∠BAD,
∴∠FAB=∠FAD,
在△FAB和△FAD中,
$\left\{\begin{array}{l}{AB=AD}\\{∠FAB=∠FAD}\\{AF=AF}\end{array}\right.$,
∴△FAB≌△FAD,
∴BF=DF,
∴∠DBF=∠FDB=45°,
∴DF⊥BC,
∵AB=AD,MA平分∠BAD,
∴BM=DM,AM⊥BD,
∵∠DAM+∠CAG=90°,∠CAG+∠ACG=90°,
∴∠MAD=∠ACG,∵AD=AC,∠AMD=∠G=90°,
∴△AMD≌△CGA,
∴AG=DM=BM=FM,CG=AM,
由(1)可知,BF=FN=AN,
∵△BFD是等腰直角三角形,FM⊥BD,
∴∠BFM=∠AFN=45°,
∴$\sqrt{2}$BF=$\sqrt{2}$AN=AF,
∴CG=AM=FM+AF=AG+$\sqrt{2}$BF.
∴$\sqrt{2}$BF+AG=CG.
(3)解:如圖3中,作AM⊥BC于M,連接DF.FA的延長線交BD于N.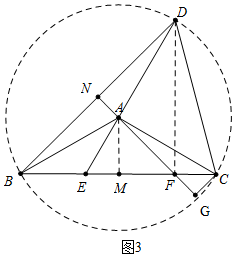
∵AB=AD,
∴AN⊥BD,BN=DN,
∴FB=FD,
∵∠CBD=$\frac{1}{2}$∠CAD=45°,
∴∠FBD=∠FDB=45°,
∴△BDF是等腰直角三角形,
∴BD=$\sqrt{2}$BF,
∵sin∠ABC=$\frac{1}{2}$,
∴∠ABC=∠ACB=∠EAM=30°,設EM=m則AE=2m,EC=4m,AM=FM=$\sqrt{3}$m,CF=CM=FM=3m-$\sqrt{3}$m,FG=$\frac{3m-\sqrt{3}m}{\sqrt{2}}$,
∴$\frac{BF•FG}{BD•AE}$=$\frac{BF}{\sqrt{2}BF}$•$\frac{\frac{3m-\sqrt{3}m}{\sqrt{2}}}{2m}$=$\frac{3-\sqrt{3}}{2}$.
點評 本題考查三角形綜合題,圓的有關知識、全等三角形的判定和性質、等腰直角三角形的性質,30度的直角三角形的性質等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,學會利用參數,用方程的思想思考問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
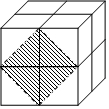 如圖,這是由8個同樣大小的立方體組成的魔方,體積為8cm3.
如圖,這是由8個同樣大小的立方體組成的魔方,體積為8cm3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
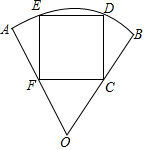 要在半徑長為1米、圓心角為60°的扇形鐵皮(如圖)上截取一塊面積盡可能大的正方形,請你設計一個截取方案(畫出示意圖),并計算這個正方形鐵皮的面積(精確到0.01).
要在半徑長為1米、圓心角為60°的扇形鐵皮(如圖)上截取一塊面積盡可能大的正方形,請你設計一個截取方案(畫出示意圖),并計算這個正方形鐵皮的面積(精確到0.01).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
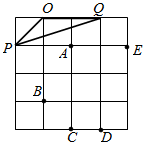 如圖,△OPQ在邊長為1個單位的方格紙中,它們的頂點在小正方形頂點位置,點A,B,C,D,E也是小正方形的頂點,從點A,B,C,D,E中選取三個點所構成的三角形與△OPQ相似,那么這個三角形是△CDB.
如圖,△OPQ在邊長為1個單位的方格紙中,它們的頂點在小正方形頂點位置,點A,B,C,D,E也是小正方形的頂點,從點A,B,C,D,E中選取三個點所構成的三角形與△OPQ相似,那么這個三角形是△CDB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股漲跌 | +1 | +1.2 | -1 | +2 | -1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com