
4.解:(1)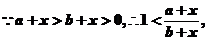
又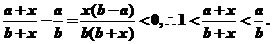
(2)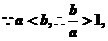 應用第(1)小題結論,得
應用第(1)小題結論,得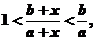 取倒數,得
取倒數,得
(3)由正弦定理,原題⇔△ABC中,求證: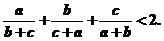
證明:由(2)的結論得,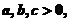 且
且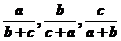 均小于1,
均小于1,
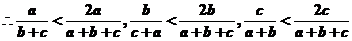 ,
,

(4)如得出:四邊形ABCD中,求證: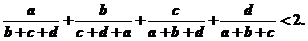 且證明正確給3分;
且證明正確給3分;
如得出:凸n邊形A1A2A3┅An中,邊長依次為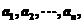 求證:
求證:
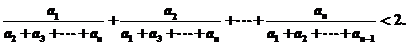 且證明正確給4分.
且證明正確給4分.
如能應用到其它內容有創意則給高分.
如得出: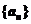 為各項為正數的等差數列,
為各項為正數的等差數列, ,求證:
,求證:
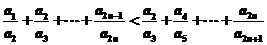 。
。
4. (上海虹口區08學年高三數學第一學期期末試卷21)(本題滿分18分)第1小題4分,第2小題4分,第3小題5分,第4小題5分.
(1)已知: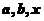 均是正數,且
均是正數,且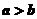 ,求證:
,求證: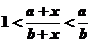 ;
;
(2)當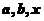 均是正數,且
均是正數,且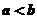 ,對真分數
,對真分數 ,給出類似上小題的結論,并予以證明;
,給出類似上小題的結論,并予以證明;
(3)證明:△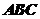 中,
中,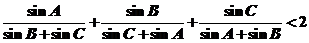 (可直接應用第(1)、(2)小題結論)
(可直接應用第(1)、(2)小題結論)
(4)自己設計一道可直接應用第(1)、(2)小題結論的不等式證明題,并寫出證明過程.
3.解:(1)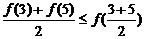 ,即
,即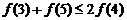
但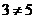 ,所以
,所以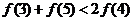
(若答案寫成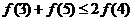 ,扣一分)
(4分)
,扣一分)
(4分)
(2)① 對于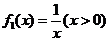 ,取
,取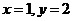 ,則
,則
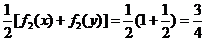
所以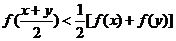 ,
,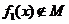 .
(6分)
.
(6分)
②對于 任取
任取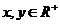 ,則
,則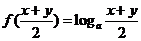
∵ 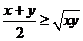 ,而函數
,而函數 是增函數
是增函數
∴ 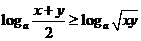 ,即
,即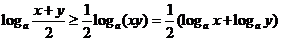
則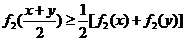 ,即
,即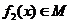 .
(10分)
.
(10分)
(3)設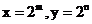 ,則
,則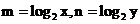 ,且m+n=1.
,且m+n=1.
由(2)知:函數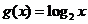 滿足
滿足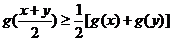 ,
,
得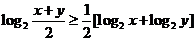 ,即
,即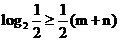 ,則
,則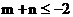 (14分)
(14分)
當且僅當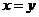 ,即
,即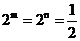 ,即m=n=-1時,m+n有最大值為-2. (16分)
,即m=n=-1時,m+n有最大值為-2. (16分)
3.(上海市奉賢區2008年高三數學聯考19)(本題滿分16分.第一小題4分,第2小題6分,第3小題6分.)
我們將具有下列性質的所有函數組成集合M:函數 ,對任意
,對任意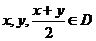 均滿足
均滿足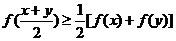 ,當且僅當
,當且僅當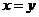 時等號成立.
時等號成立.
若定義在(0,+∞)上的函數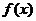 ∈M,試比較
∈M,試比較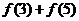 與
與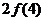 大小.
大小.
給定兩個函數: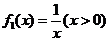 ,
, .
.
證明: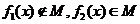 .
.
試利用(2)的結論解決下列問題:若實數m、n滿足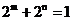 ,求m+n的最大值.
,求m+n的最大值.
2.解: 當 時,P=
時,P=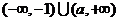
當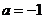 時,P=
時,P=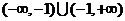
當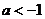 時,P=
時,P=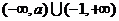 ----------6分
----------6分
Q: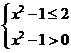
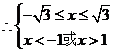
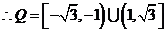 ------9分
------9分
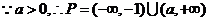 ---------10分
---------10分
若Q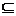 P
P 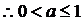 ---------12分
---------12分
2.(上海市八校2008學年第一學期高三數學考試試卷17)(本小題滿分12分)
關于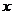 的不等式
的不等式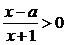 的解集為P,不等式
的解集為P,不等式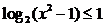 的解集為Q. 若Q
的解集為Q. 若Q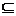 P, 求正數
P, 求正數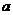 的取值范圍
的取值范圍
1. 解:設新電價為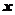 元/千瓦時
元/千瓦時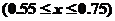 ,則新增用電量為
,則新增用電量為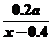 千瓦時.
千瓦時.
依題意,有
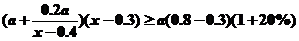 ,
,
即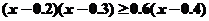 ,
,
整理,得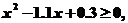
解此不等式,得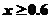 或
或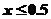 ,
,
又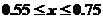 ,
,
所以,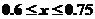 ,
,
因此,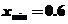 ,即電價最低為
,即電價最低為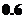 元/千瓦時,可保證電力部門的收益比上一年度至少增加20%.
元/千瓦時,可保證電力部門的收益比上一年度至少增加20%.
1(上海市盧灣區2008學年高三年級第一次質量調研第16題)(本題滿分10分)
解不等式: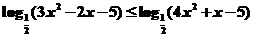 .
.
答案:解:原不等式的解集為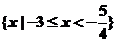
2 (2008學年度第一學期上海市普陀區高三年級質量調研第17題)(本題滿分14分,第1小題6分,第2小題8分)
已知關于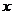 的不等式
的不等式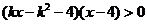 ,其中
,其中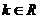 .
.
(1)
當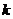 變化時,試求不等式的解集
變化時,試求不等式的解集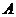 ;
;
(2)
對于不等式的解集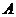 ,若滿足
,若滿足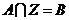 (其中
(其中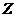 為整數集). 試探究集合
為整數集). 試探究集合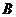 能否為有限集?若能,求出使得集合
能否為有限集?若能,求出使得集合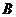 中元素個數最少的
中元素個數最少的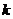 的所有取值,并用列舉法表示集合
的所有取值,并用列舉法表示集合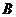 ;若不能,請說明理由.
;若不能,請說明理由.
答案:
解:(1)當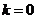 時,
時,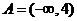 ;
;
當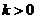 且
且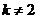 時,
時,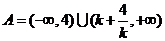 ;
;
當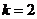 時,
時,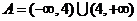 ;(不單獨分析
;(不單獨分析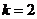 時的情況不扣分)
時的情況不扣分)
當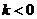 時,
時,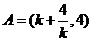 .
.
(2)
由(1)知:當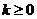 時,集合
時,集合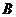 中的元素的個數無限;
中的元素的個數無限;
當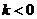 時,集合
時,集合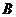 中的元素的個數有限,此時集合
中的元素的個數有限,此時集合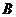 為有限集.
為有限集.
因為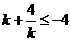 ,當且僅當
,當且僅當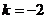 時取等號,
時取等號,
所以當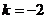 時,集合
時,集合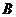 的元素個數最少.
的元素個數最少.
此時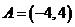 ,故集合
,故集合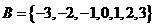 .
.
3 (靜安區部分中學08-09學年度第一學期期中數學卷第19題)(本題滿分14分)本題共有2個小題,第1小題滿分7分,第2小題滿分7分.
某商品每件成本價80元,售價100元,每天售出100件.若售價降低x成(1成=10%),售出商品數量就增加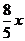 成,要求售價不能低于成本價.
成,要求售價不能低于成本價.
(1)設該商店一天的營業額為y,試求y與x之間的函數關系式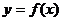 ,并寫出定義域;
,并寫出定義域;
(2)若再要求該商品一天營業額至少10260元,求x的取值范圍.
答案:(1)依題意,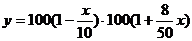 ;3分
;3分
又售價不能低于成本價,所以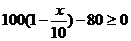 .2分
.2分
所以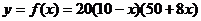 ,定義域為
,定義域為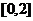 .2分
.2分
(2)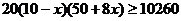 ,化簡得:
,化簡得: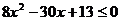 3分
3分
解得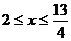 .3分
.3分
所以x的取值范圍是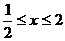 .1分
.1分
4 (靜安區部分中學08-09學年度第一學期期中數學卷第20題)(本題滿分16分)本題共有2個小題,第1小題滿分8分,第2小題滿分8分.
已知函數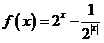 .
.
(1)(理)設集合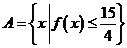 ,
,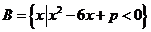 ,若
,若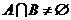 ,求實數
,求實數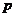 的取值范圍;
的取值范圍;
(文)若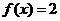 ,求
,求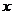 的值;
的值;
(2)若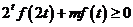 對于
對于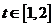 恒成立,求實數
恒成立,求實數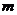 的取值范圍.
的取值范圍.
答案:(1)(理)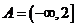 3分
3分
設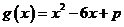 ,因為
,因為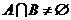 ,所以
,所以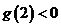
進而 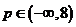 5分
5分
(文)(1)當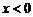 時,
時,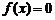 ;當
;當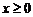 時,
時,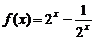 . ……
2分
. ……
2分
由條件可知 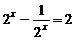 ,即
,即 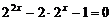 ,
,
解得 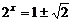 .
…… 4分
.
…… 4分
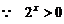 ,
,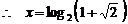 .
…… 2分
.
…… 2分
(2)因為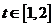 ,所以
,所以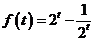 ,
2分
,
2分
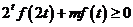 恒成立即
恒成立即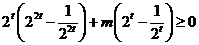 恒成立,
恒成立,
即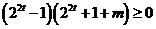 ,
,
因為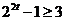 ,所以
,所以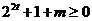 恒成立,
3分
恒成立,
3分
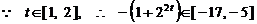 ,
,
即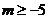 3分
3分
5 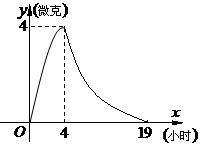 某醫藥研究所開發一種新藥,據監測:服藥后每毫升血液中的含藥量
某醫藥研究所開發一種新藥,據監測:服藥后每毫升血液中的含藥量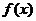 與時間
與時間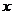 之間滿足如圖所示曲線.當
之間滿足如圖所示曲線.當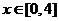 時,所示的曲線是二次函數圖像的一部分,滿足
時,所示的曲線是二次函數圖像的一部分,滿足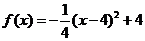 ,當
,當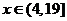 時,所示的曲線是函數
時,所示的曲線是函數 的圖像的一部分.據測定:每毫升血液中含藥量不少于
的圖像的一部分.據測定:每毫升血液中含藥量不少于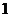 微克時治療疾病有效.請你算一下,服用這種藥一次大概能維持多長的有效時間?(精確到
微克時治療疾病有效.請你算一下,服用這種藥一次大概能維持多長的有效時間?(精確到 小時)
小時)
答案:由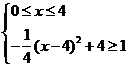 ,解得:
,解得: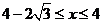 ①
(4分)
①
(4分)
由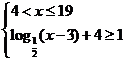 ,解得:
,解得: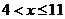 ②
(8分)
②
(8分)
由①、②知: , (10分)
, (10分)
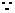
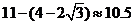 ,
(12分)
,
(12分)
∴服用這種藥一次大概能維持的有效時間為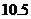 小時.
(14分)
小時.
(14分)
6 (上海市青浦區2008學年高三年級第一次質量調研第19題)(本題滿分14分)
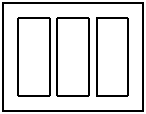
迎世博,要設計如圖的一張矩形廣告,該廣告含有大小相等的左中右三個矩形欄目,這三欄的面積之和為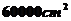 ,四周空白的寬度為
,四周空白的寬度為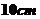 ,欄與欄之間的中縫空白的寬度為
,欄與欄之間的中縫空白的寬度為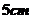 ,怎樣確定廣告矩形欄目高與寬的尺寸(單位:
,怎樣確定廣告矩形欄目高與寬的尺寸(單位: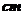 ),能使整個矩形廣告面積最小.
),能使整個矩形廣告面積最小.
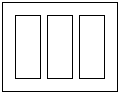
答案:解:設矩形欄目的高為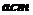 ,寬為
,寬為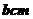 ,則
,則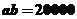 ,
,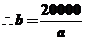
 廣告的高為
廣告的高為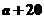 ,寬為
,寬為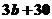 (其中
(其中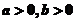 )
)
廣告的面積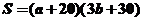
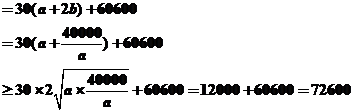
當且僅當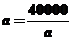 ,即
,即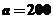 時,取等號,此時
時,取等號,此時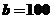 .
.
故當廣告的高為200cm,寬為100cm時,可使廣告的面積最小.
1.(上海市黃浦區2008學年高三年級第一次質量調研19)(本題滿分12分)
某城市上年度電價為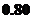 元/千瓦時,年用電量為
元/千瓦時,年用電量為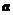 千瓦時.本年度計劃將電價降到
千瓦時.本年度計劃將電價降到 元/千瓦時-
元/千瓦時-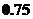 元/千瓦時之間,而居民用戶期望電價為
元/千瓦時之間,而居民用戶期望電價為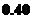 元/千瓦時(該市電力成本價為
元/千瓦時(該市電力成本價為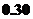 元/千瓦時)
元/千瓦時)
經測算,下調電價后,該城市新增用電量與實際電價和用戶期望電價之差成反比,比例系數為 .試問當地電價最低為多少時,可保證電力部門的收益比上年度至少增加
.試問當地電價最低為多少時,可保證電力部門的收益比上年度至少增加 .
.
16. ( (上海市青浦區2008學年高三年級第一次質量調研第11題) 設函數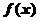 的定義域為
的定義域為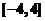 ,其圖像如下圖,那么不等式
,其圖像如下圖,那么不等式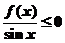 的解集為____________.答案:
的解集為____________.答案: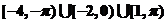
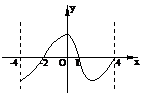
15. (浦東新區2008學年度第一學期期末質量抽測卷數學理科第12題)研究問題:“已知關于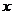 的不等式
的不等式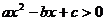 的解集為
的解集為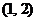 ,解關于
,解關于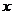 的不等式
的不等式
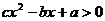 ”,有如下解法:
”,有如下解法:
 解:由
解:由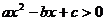
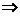
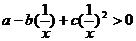 ,令
,令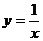 ,則
,則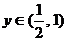 ,
,
所以不等式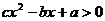 的解集為
的解集為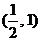 .
.
參考上述解法,已知關于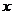 的不等式
的不等式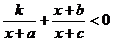 的解集為
的解集為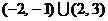 ,則
,則
關于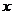 的不等式
的不等式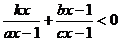 的解集為 .
的解集為 .
答案:
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com