
15. 過長方體一個頂點的三條棱長為3、4、5, 且它的八個頂點都在同一球面上,這個球的表面積是________.
講解 長方體的對角線就是外接球的直徑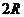 , 即有
, 即有
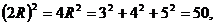
從而 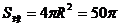 ,故應填
,故應填
14. 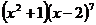 的展開式中
的展開式中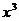 的系數是
的系數是
講解 由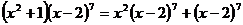 知,所求系數應為
知,所求系數應為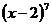 的x項的系數與
的x項的系數與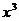 項的系數的和,即有
項的系數的和,即有
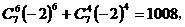
故應填1008.
13.某商場開展促銷活動,設計一種對獎券,號碼從000000到999999. 若號碼的奇位數字是不同的奇數,偶位數字均為偶數時,為中獎號碼,則中獎面(即中獎號碼占全部號碼的百分比)為 .
講解 中獎號碼的排列方法是: 奇位數字上排不同的奇數有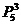 種方法,偶位數字上排偶數的方法有
種方法,偶位數字上排偶數的方法有 ,從而中獎號碼共有
,從而中獎號碼共有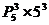 種,于是中獎面為
種,于是中獎面為
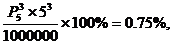
故應填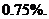
12.以下四個命題:
①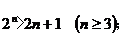
②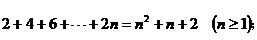
③凸n邊形內角和為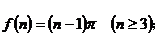 ④凸n邊形對角線的條數是
④凸n邊形對角線的條數是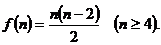
其中滿足“假設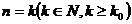 時命題成立,則當n=k+1時命題也成立’’.但不滿足“當
時命題成立,則當n=k+1時命題也成立’’.但不滿足“當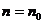 (
(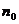 是題中給定的n的初始值)時命題成立”的命題序號是 .
是題中給定的n的初始值)時命題成立”的命題序號是 .
講解 ①當n=3時,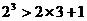 ,不等式成立;
,不等式成立;
② 當n=1時,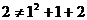 ,但假設n=k時等式成立,則
,但假設n=k時等式成立,則
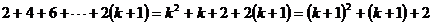 ;
;
③ 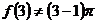 ,但假設
,但假設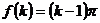 成立,則
成立,則
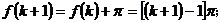
④ 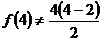 ,假設
,假設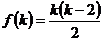 成立,則
成立,則
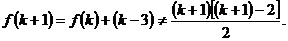
故應填②③.
11.
列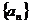 中,
中,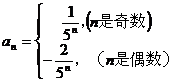
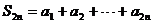 , 則
, 則
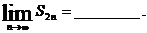

講解 分類求和,得
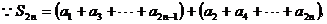

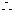
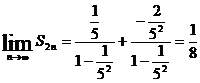 ,故應填
,故應填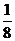 .
.
10. 已知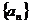 是公差不為零的等差數列,如果
是公差不為零的等差數列,如果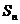 是
是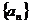 的前n項和,那么
的前n項和,那么
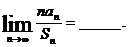

講解 特別取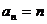 ,有
,有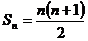 ,于是有
,于是有
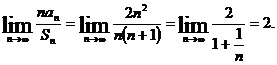 故應填2.
故應填2.
9.設非零復數 滿足
滿足 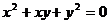 ,則代數式
,則代數式 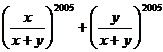 的值是____________.
的值是____________.
講解 將已知方程變形為 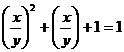 ,
,
解這個一元二次方程,得
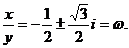

顯然有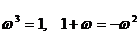 , 而
, 而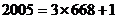 ,于是
,于是
原式=

=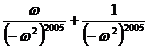

=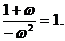

在上述解法中,“兩邊同除”的手法達到了集中變量的目的,這是減少變元的一個上策,值得重視.
8.
設復數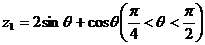 在復平面上對應向量
在復平面上對應向量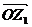 ,
, 將
將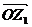 按順時針方向旋轉
按順時針方向旋轉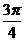 后得到向量
后得到向量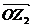 ,
,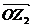 對應的復數為
對應的復數為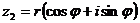 ,則
,則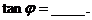

講解 應用復數乘法的幾何意義,得
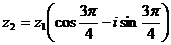

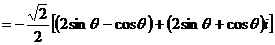 ,
,
于是 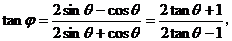

故應填 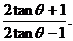

7.
如果函數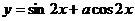 的圖象關于直線
的圖象關于直線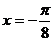 對稱,那么
對稱,那么

講解 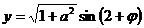 ,其中
,其中 .
.
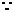
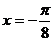 是已知函數的對稱軸,
是已知函數的對稱軸,
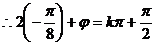 ,
,
即 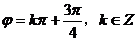 ,
,
于是 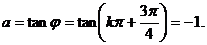 故應填
故應填 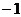 .
.
在解題的過程中,我們用到如下小結論:
函數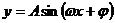 和
和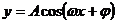 的圖象關于過最值點且垂直于x軸的直線分別成軸對稱圖形.
的圖象關于過最值點且垂直于x軸的直線分別成軸對稱圖形.
6.
不等式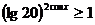 (
( )的解集為
)的解集為 .
.
講解 注意到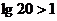 ,于是原不等式可變形為
,于是原不等式可變形為
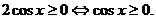

而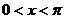 ,所以
,所以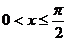 ,故應填
,故應填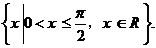

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com