
2.一元一次不等式
解一元一次不等式(組)及一元二次不等式(組)是解其他各類不等式的基礎,必須熟練掌握,靈活應用。
 情況分別解之。
情況分別解之。
解不等式是求定義域、值域、參數的取值范圍時的重要手段,與“等式變形”并列的“不等式的變形”,是研究數學的基本手段之一。
高考試題中,對解不等式有較高的要求,近兩年不等式知識占相當大的比例。
1.不等式同解變形
(1)同解不等式((1) 與
與 同解;
同解;
(2)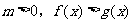 與
與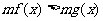 同解,
同解,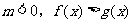 與
與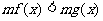 同解;
同解;
(3)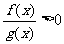 與
與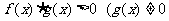 同解);
同解);
3.分析法
證明不等式時,有時可以從求證的不等式出發,分析使這個不等式成立的充分條件,把證明不等式轉化為判定這些充分條件是否具備的問題,如果能夠肯定這些充分條件都已具備,那么就可以斷定原不等式成立,這種方法通常叫做分析法。
注意:
(1)“分析法”是從求證的不等式出發,分析使這個不等式成立的充分條件,把證明不等式轉化為判定這些充分條件是否具備的問題,即“執果索因”;
(2)綜合過程有時正好是分析過程的逆推,所以常用分析法探索證明的途徑,然后用綜合法的形式寫出證明過程。
2.綜合法
利用某些已經證明過的不等式(例如算術平均數與幾何平均數的定理)和不等式的性質,推導出所要證明的不等式,這個證明方法叫綜合法;利用某些已經證明過的不等式和不等式的性質時要注意它們各自成立的條件。
綜合法證明不等式的邏輯關系是: ,及從已知條件
,及從已知條件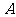 出發,逐步推演不等式成立的必要條件,推導出所要證明的結論
出發,逐步推演不等式成立的必要條件,推導出所要證明的結論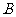 。
。
1.比較法
比較法證明不等式的一般步驟:作差-變形-判斷-結論;為了判斷作差后的符號,有時要把這個差變形為一個常數,或者變形為一個常數與一個或幾個平方和的形式,也可變形為幾個因式的積的形式,以便判斷其正負。
在一條平直的南北方向的公路上,有甲、乙兩輛汽車順序向北行駛,甲車比乙車快。問:(1)以什么為參照物,兩輛車均向北運動?
(2)若以甲車為參照物,乙車向什么方向運動?
(3)若以乙車為參照物,甲車向什么方向運動?
(4)以什么為參照物,兩輛車均向南運動。
6、有兩座相距S=1000m的大山,有人在兩座大山之間大喊一聲,先后聽到由兩山傳來的兩個回聲,時間相隔4s,設聲速V=340m/s。求這個人到兩山的距離為多少?
5、汽車從甲站出發頭20s前進了100m,然后以36km/h的速度勻速行駛2min,以后又用4min前進了50m,到了乙站停車。求:(1)汽車在前20s內的平均速度。(2)汽車在最后4秒內的平均速度。(3)汽車在整個路程中行駛的平均速度。
4、汽車在平直公路上行駛,C是A、B兩站的中點,汽車在AC段運動時的平均速度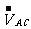 =20km/h,在CB段運動時的平均速度
=20km/h,在CB段運動時的平均速度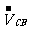 =30km/h,求汽車在AB段運動時的平均速度
=30km/h,求汽車在AB段運動時的平均速度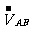 為多少?
為多少?
3、一支隊伍長50m,以5m/s的速度通過一座100m長的橋,從第一人上橋到最后一人離開橋所用的時間為多少?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com