
7. 已知數列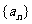 滿足
滿足 ,則
,則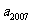 =
=
6. 在等比數列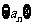 中,
中,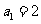 ,前
,前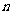 項和為
項和為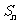 ,若數列
,若數列 也是等比數列,則
也是等比數列,則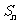 等于
等于
5. 已知等差數列{an}的前n項和為Sn,若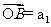
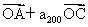 ,且A、B、C三點共線(該直線不過原點O),則S200=
,且A、B、C三點共線(該直線不過原點O),則S200=
4. 若互不相等的實數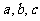 成等差數列,
成等差數列,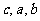 成等比數列,且
成等比數列,且 ,則
,則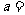
3. 已知某等差數列共有10項,其奇數項之和為15,偶數項之和為30,則其公差為
2. 在等差數列{a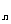 }中,已知a
}中,已知a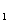 =2,a
=2,a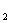 +a
+a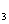 =13,則a
=13,則a +a
+a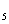 +a
+a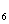 等于
等于
1. 如果-1,a, b,c,-9成等比數列,那么b=
2. 解綜合題要總攬全局,尤其要注意上一問的結論可作為下面論證的已知條件,在后面求解的過程中適時應用.
話題3:函數與數列的綜合題
數列是一特殊的函數,其定義域為正整數集,且是自變量從小到大變化時函數值的序列。注意深刻理解函數性質對數列的影響,分析題目特征,探尋解題切入點.
例6. (2006湖北卷)已知二次函數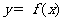 的圖像經過坐標原點,其導函數為
的圖像經過坐標原點,其導函數為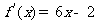 ,數列
,數列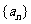 的前n項和為
的前n項和為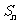 ,點(n,
,點(n,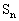 )(n
)(n )均在函數
)均在函數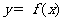 的圖像上。(Ⅰ)、求數列
的圖像上。(Ⅰ)、求數列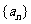 的通項公式;(Ⅱ)、設
的通項公式;(Ⅱ)、設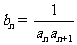 ,
,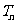 是數列
是數列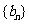 的前n項和,求使得
的前n項和,求使得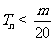 對所有
對所有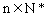 都成立的最小正整數m;
都成立的最小正整數m;
點評:本題考查二次函數、等差數列、數列求和、不等式等基礎知識和基本的運算技能,考查分析問題的能力和推理能力。
解:(Ⅰ)設二次函數為f(x)=ax2+bx (a≠0) ,則 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因為點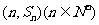 均在函數
均在函數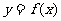 的圖像上,所以
的圖像上,所以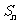 =3n2-2n.
=3n2-2n.
當n≥2時,an=Sn-Sn-1=(3n2-2n)- =6n-5.
=6n-5.
當n=1時,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (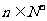 )
)
(Ⅱ)由(Ⅰ)得知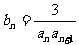 =
=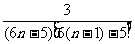 =
=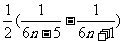 ,
,
故Tn= =
=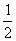
 =
=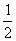 (1-
(1-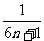 ).
).
因此,要使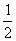 (1-
(1-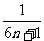 )<
)< (
(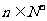 )成立的m必須且僅需滿足
)成立的m必須且僅需滿足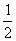 ≤
≤ ,即m≥10,所以滿足要求的最小正整數m為10.
,即m≥10,所以滿足要求的最小正整數m為10.
例7. 設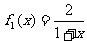 ,定義
,定義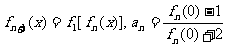 ,其中n∈N*.
,其中n∈N*.
(1)求數列{an}的通項公式;
(2)若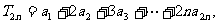 求
求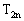 前2n項的和。
前2n項的和。
解:(1)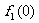 =2,
=2,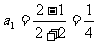 ,
,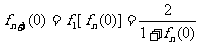 ,
,
∴
∴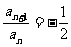 ,∴數列{an}是首項為
,∴數列{an}是首項為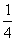 ,公比為
,公比為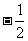 的等比數列,
的等比數列,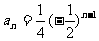
(2)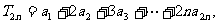
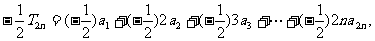
兩式相減得:
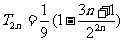
例8. (湖北卷)設數列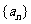 的前n項和為
的前n項和為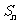 ,點
,點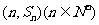 均在函數y=3x-2的圖像上。
均在函數y=3x-2的圖像上。
(Ⅰ)求數列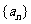 的通項公式;(Ⅱ)設
的通項公式;(Ⅱ)設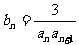 ,
,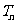 是數列
是數列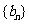 的前n項和,求使得
的前n項和,求使得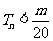 對所有
對所有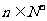 都成立的最小正整數m。
都成立的最小正整數m。
本小題主要是考查等差數列、數列求和、不等式等基礎知識和基本的運算技能,考查分析問題的能力和推理能力。
解:(I)依題意得,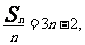 即
即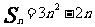 。
。
當n≥2時,a ;
;
當n=1時,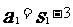 ×
×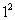 -2×1-1-6×1-5
-2×1-1-6×1-5
所以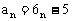 (
(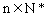 )。
)。
(II)由(I)得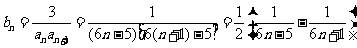 ,
,
故 。
。
因此,使得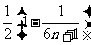 ﹤
﹤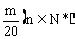 成立的m必須滿足
成立的m必須滿足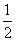 ≤
≤ ,即m≥10,故滿足要求的最小整數m為10。
,即m≥10,故滿足要求的最小整數m為10。
話題4:數列與解析幾何
數列與解析幾何綜合題,是今后高考命題的重點內容之一,求解時要充分利用數列、解析幾何的概念、性質,并結合圖形求解.
例9. 在直角坐標平面上有一點列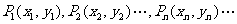 ,對一切正整數
,對一切正整數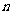 ,點
,點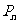 位于函數
位于函數 的圖像上,且
的圖像上,且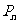 的橫坐標構成以
的橫坐標構成以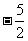 為首項,
為首項,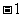 為公差的等差數列
為公差的等差數列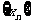 .
.
⑴求點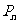 的坐標;⑵設拋物線列
的坐標;⑵設拋物線列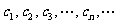 中的每一條的對稱軸都垂直于
中的每一條的對稱軸都垂直于 軸,第
軸,第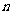 條拋物線
條拋物線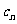 的頂點為
的頂點為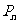 ,且過點
,且過點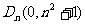 ,記與拋物線
,記與拋物線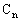 相切于
相切于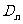 的直線的斜率為
的直線的斜率為 ,求:
,求: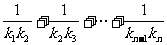 .
.
解:(1)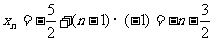
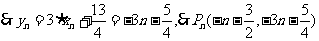
(2)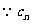 的對稱軸垂直于
的對稱軸垂直于 軸,且頂點為
軸,且頂點為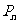 .
.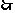 設
設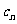 的方程為:
的方程為: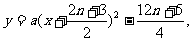
把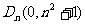 代入上式,得
代入上式,得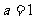 ,
,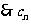 的方程為:
的方程為: 。
。
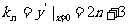 ,
,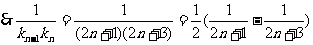
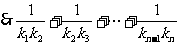
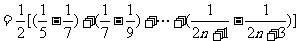
=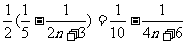
點評:本例為數列與解析幾何的綜合題,難度較大。(1)、(2)兩問運用幾何知識算出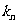 .
.
例10. 已知拋物線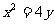 ,過原點作斜率1的直線交拋物線于第一象限內一點
,過原點作斜率1的直線交拋物線于第一象限內一點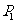 ,又過點
,又過點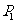 作斜率為
作斜率為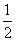 的直線交拋物線于點
的直線交拋物線于點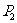 ,再過
,再過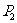 作斜率為
作斜率為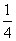 的直線交拋物線于點
的直線交拋物線于點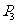 ,
, ,如此繼續,一般地,過點
,如此繼續,一般地,過點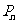 作斜率為
作斜率為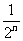 的直線交拋物線于點
的直線交拋物線于點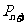 ,設點
,設點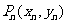 .
.
令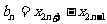 ,求證:數列
,求證:數列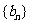 是等比數列. 并求數列
是等比數列. 并求數列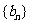 的前
的前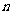 項和
項和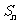
解:因為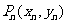 、
、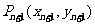 在拋物線上,故
在拋物線上,故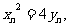 ①
①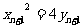 ②,又因為直線
②,又因為直線 的斜率為
的斜率為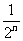 ,即
,即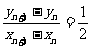 ,①②代入可得
,①②代入可得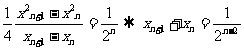
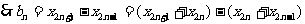
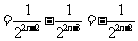 , 故
, 故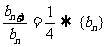 是以
是以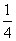
為公比的等比數列;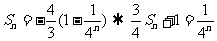 ,
,
話題5:數列創新題
例11.(安徽卷)數列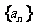 的前
的前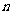 項和為
項和為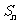 ,已知
,已知
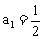 ,
, ,
,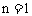 ,2,…
,2,…
(Ⅰ)寫出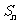 與
與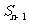 的遞推關系式(
的遞推關系式(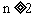 ),并求
),并求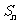 關于
關于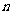 的表達式;
的表達式;
(Ⅱ)設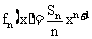 ,
,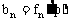 (
(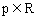 ),求數列
),求數列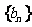 的前
的前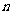 項和
項和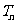 。
。
解:由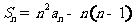 (
(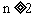 )得:
)得: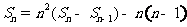 ,即
,即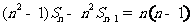 ,所以
,所以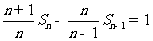 ,對
,對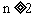 成立。
成立。
由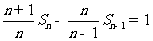 ,
,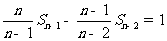 ,…,
,…,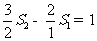 相加得:
相加得: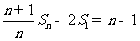 ,又
,又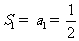 ,所以
,所以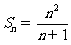 ,當
,當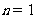 時也成立。
時也成立。
(Ⅱ)由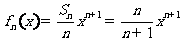 ,得
,得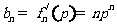 。
。
而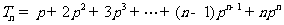 ,
,
 ,
,
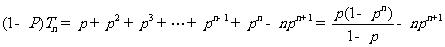
例12. (福建卷)已知數列{an}滿足a1=a, an+1=1+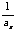 我們知道當a取不同的值時,得到不同的數列,如當a=1時,得到無窮數列:
我們知道當a取不同的值時,得到不同的數列,如當a=1時,得到無窮數列:
(Ⅰ)求當a為何值時a4=0;(Ⅱ)設數列{bn}滿足b1=-1, bn+1=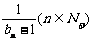 ,求證:a取數列{bn}中的任一個數,都可以得到一個有窮數列{an};
,求證:a取數列{bn}中的任一個數,都可以得到一個有窮數列{an};
(I)解法一: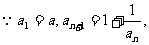
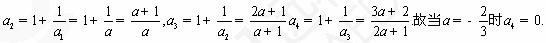

故a取數列{bn}中的任一個數,都可以得到一個有窮數列{an}
例13. (全國卷III) 在等差數列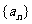 中,公差
中,公差 的等比中項.
的等比中項.
已知數列 成等比數列,求數列
成等比數列,求數列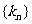 的通項
的通項
解:由題意得: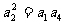 即
即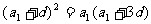
又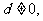
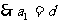
又 成等比數列,
成等比數列,
∴該數列的公比為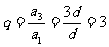 ,
,
所以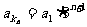
又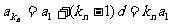
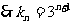 所以數列
所以數列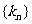 的通項為
的通項為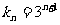
話題6:永遠的遞推
例14. 在數列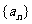 中,
中,
(1)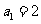 ,
,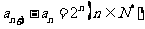 ,則通項公式
,則通項公式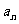 = _____
= _____
(2)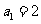 ,
,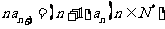 ,則通項公式
,則通項公式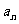 = _____
= _____
(3)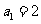 ,
,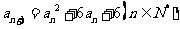 ,則通項公式
,則通項公式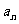 = _____
= _____
(4)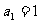 ,當
,當 時,
時,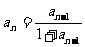 ,則通項公式
,則通項公式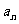 = _____
= _____
(5)已知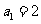 ,
,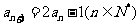 ,則通項公式
,則通項公式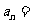
(6)設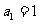 ,且
,且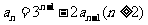 . 則通項公式
. 則通項公式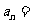
(7)設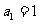 ,且
,且 . 則通項公式
. 則通項公式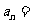
解:(1)迭加得:
(2)迭乘得: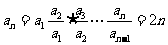
(3)迭代得:
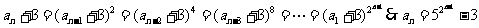
(4)取倒數得等差數列: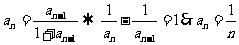
(5)配方得等比數列: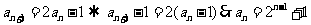
(6)配方得等比數列:
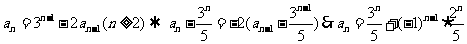
(7)同除以2n得等差數列:
[模擬試題]
4. 解綜合題的成敗在于審清題目,弄懂來龍去脈,透過給定信息的表象,抓住問題的本質,揭示問題的內在聯系和隱含條件,明確解題方向,形成解題策略.
[典型例題]
話題1:等差、等比數列的項與和的特征問題
例1. (四川卷)數列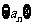 的前
的前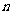 項和記為
項和記為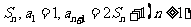 (Ⅰ)求
(Ⅰ)求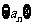 的通項公式;(Ⅱ)等差數列
的通項公式;(Ⅱ)等差數列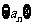 的各項為正,其前
的各項為正,其前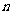 項和為
項和為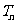 ,且
,且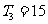 ,又
,又 成等比數列,求
成等比數列,求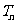
解:(Ⅰ)由 可得
可得 ,兩式相減得
,兩式相減得
又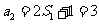 ∴
∴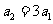 故
故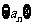 是首項為
是首項為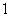 ,公比為
,公比為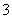 的等比數列 ∴
的等比數列 ∴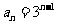
(Ⅱ)設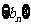 的公比為
的公比為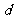 ,由
,由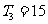 得,可得
得,可得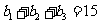 ,可得
,可得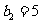
故可設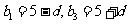 又
又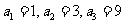
由題意可得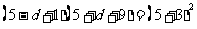 解得
解得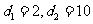
∵等差數列 的各項為正,∴
的各項為正,∴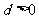 ∴
∴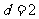 ∴
∴
例2. (上海卷)設數列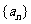 的前
的前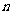 項和為
項和為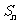 ,且對任意正整數
,且對任意正整數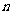 ,
,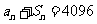 。(1)求數列
。(1)求數列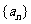 的通項公式?(2)設數列
的通項公式?(2)設數列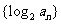 的前
的前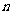 項和為
項和為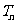 ,對數列
,對數列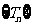 ,從第幾項起
,從第幾項起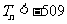 ?
?
解:(1) ∵an+ Sn=4096, ∴a1+ S1=4096, a1 =2048.
當n≥2時, an= Sn-Sn-1=(4096-an)-(4096-an-1)= an-1-an
∴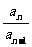 =
=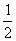 ,an=2048(
,an=2048(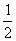 )n-1.
)n-1.
(2) ∵log2an=log2[2048(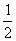 )n-1]=12-n, ∴Tn=
)n-1]=12-n, ∴Tn=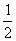 (-n2+23n).
(-n2+23n).
由Tn<-509,解得n>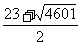 ,而n是正整數,于是,n≥46. ∴從第46項起Tn<-509.
,而n是正整數,于是,n≥46. ∴從第46項起Tn<-509.
例3. (全國卷Ⅰ) 設正項等比數列 的首項
的首項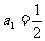 ,前n項和為
,前n項和為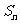 ,且
,且 。(Ⅰ)求
。(Ⅰ)求 的通項公式;(Ⅱ)求
的通項公式;(Ⅱ)求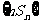 的前n項和
的前n項和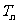 。
。
解:(Ⅰ)由 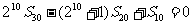 得
得 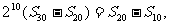
即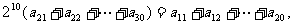
可得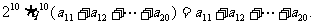
因為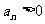 ,所以
,所以 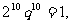 解得
解得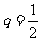 ,因而
,因而 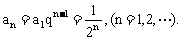
(Ⅱ)因為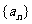 是首項
是首項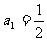 、公比
、公比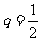 的等比數列,故
的等比數列,故
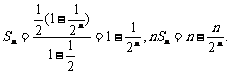
則數列 的前n項和
的前n項和 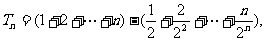
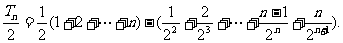
前兩式相減,得 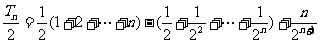
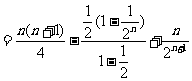 即
即 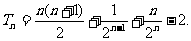
話題2:等差、等比數列的判定問題.
例4. (上海卷)已知有窮數列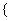
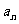
 共有2
共有2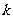 項(整數
項(整數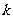 ≥2),首項
≥2),首項 =2. 設該數列的前
=2. 設該數列的前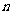 項和為
項和為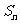 ,且
,且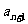 =
=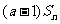 +2(
+2(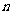 =1,2,…,2
=1,2,…,2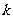 -1),其中常數
-1),其中常數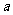 >1.
>1.
(1)求證:數列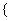
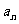
 是等比數列;(2)若
是等比數列;(2)若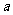 =2
=2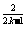 ,數列
,數列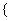
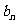
 滿足
滿足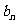 =
=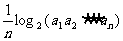 (
(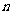 =1,2,…,2
=1,2,…,2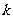 ),求數列
),求數列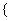
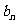
 的通項公式;
的通項公式;
(3)若(2)中的數列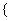
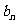
 滿足不等式|
滿足不等式|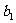 -
-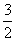 |+|
|+|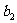 -
-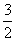 |+…+|
|+…+|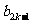 -
-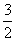 |+|
|+| -
-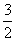 |≤4,求
|≤4,求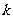 的值.
的值.
(1) 證明:當n=1時,a2=2a,則 =a;
=a;
2≤n≤2k-1時, an+1=(a-1) Sn+2, an=(a-1) Sn-1+2,
an+1-an=(a-1) an, ∴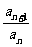 =a, ∴數列{an}是等比數列.
=a, ∴數列{an}是等比數列.
(2) 解:由(1) 得an=2a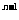 , ∴a1a2…an=2
, ∴a1a2…an=2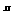 a
a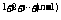 =2
=2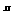 a
a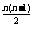 =2
=2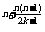 ,
,
bn=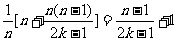 (n=1,2,…,2k).
(n=1,2,…,2k).
(3)設bn≤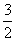 ,解得n≤k+
,解得n≤k+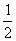 ,又n是正整數,于是當n≤k時, bn<
,又n是正整數,于是當n≤k時, bn<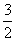 ;
;
當n≥k+1時, bn>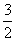 .
.
原式=(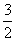 -b1)+(
-b1)+(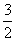 -b2)+…+(
-b2)+…+(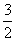 -bk)+(bk+1-
-bk)+(bk+1-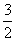 )+…+(b2k-
)+…+(b2k-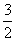 )
)
=(bk+1+…+b2k)-(b1+…+bk)
=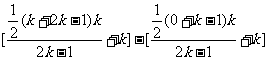 =
=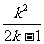 .
.
當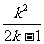 ≤4,得k2-8k+4≤0, 4-2
≤4,得k2-8k+4≤0, 4-2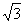 ≤k≤4+2
≤k≤4+2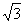 ,又k≥2,
,又k≥2,
∴當k=2,3,4,5,6,7時,原不等式成立.
例5. 已知數列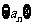 中,
中,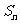 是其前
是其前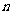 項和,并且
項和,并且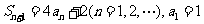 ,⑴設數列
,⑴設數列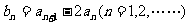 ,求證:數列
,求證:數列 是等比數列;⑵設數列
是等比數列;⑵設數列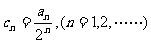 ,求證:數列
,求證:數列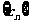 是等差數列;⑶求數列
是等差數列;⑶求數列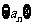 的通項公式及前
的通項公式及前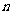 項和。
項和。
分析:由于{b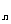 }和{c
}和{c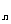 }中的項都和{a
}中的項都和{a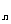 }中的項有關,{a
}中的項有關,{a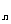 }中又有S
}中又有S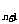 =4a
=4a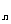 +2,可由S
+2,可由S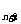 -S
-S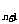 作切入點探索解題的途徑.
作切入點探索解題的途徑.
[注2]本題立意與2007年高考題文科20題結構相似.
解:(1)由S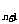 =4a
=4a ,S
,S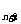 =4a
=4a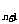 +2,兩式相減,得S
+2,兩式相減,得S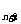 -S
-S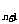 =4(a
=4(a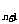 -a
-a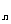 ),即a
),即a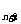 =4a
=4a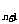 -4a
-4a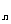 . (根據b
. (根據b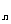 的構造,如何把該式表示成b
的構造,如何把該式表示成b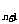 與b
與b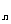 的關系是證明的關鍵,注意加強恒等變形能力的訓練)
的關系是證明的關鍵,注意加強恒等變形能力的訓練)
a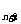 -2a
-2a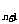 =2(a
=2(a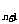 -2a
-2a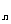 ),又b
),又b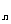 =a
=a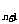 -2a
-2a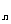 ,所以b
,所以b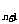 =2b
=2b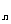 ①
①
已知S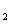 =4a
=4a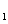 +2,a
+2,a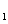 =1,a
=1,a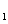 +a
+a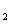 =4a
=4a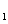 +2,解得a
+2,解得a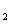 =5,b
=5,b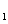 =a
=a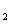 -2a
-2a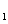 =3 ②
=3 ②
由①和②得,數列{b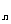 }是首項為3,公比為2的等比數列,故b
}是首項為3,公比為2的等比數列,故b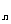 =3·2
=3·2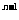 .
.
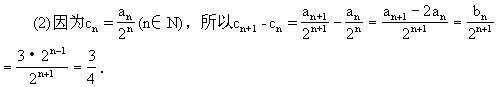

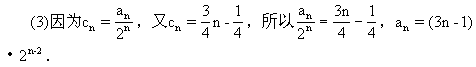
當n≥2時,S =4a
=4a +2=2
+2=2 (3n-4)+2;當n=1時,S
(3n-4)+2;當n=1時,S =a
=a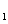 =1也適合上式.
=1也適合上式.
綜上可知,所求的前n項和為S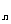 =2
=2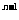 (3n-4)+2.
(3n-4)+2.
說明:1. 本例主要復習用等差、等比數列的定義證明一個數列為等差,等比數列,求數列的通項公式與前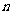 項和。解決本題的關鍵在于由條件
項和。解決本題的關鍵在于由條件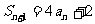 得出遞推公式。
得出遞推公式。
3. 注意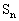 與
與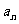 之間關系的轉化。如:
之間關系的轉化。如: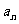 =
=
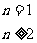 ,
,
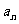 =
=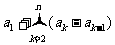 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com