
題目列表(包括答案和解析)
4.不等式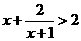 的解集是 ( )
的解集是 ( )
A. B.
B.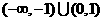
C. D.
D.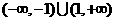
3.圓 的圓心到直線
的圓心到直線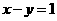 的距離為 ( )
的距離為 ( )
A.2 B.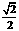 C.1
D.
C.1
D.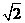
2.函數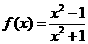 , 則
, 則 ( )
( )
A.1 B.-1 C.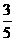 D.
D.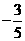
1.函數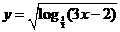 的定義域是 (
)
的定義域是 (
)
A.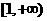 B.
B. C.[
C.[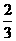 ,1] D.(
,1] D.(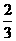 ,1
,1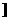
(17)已知f(x)=Asin(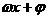 )(A>0,
)(A>0, >0,0<
>0,0<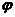 <
<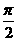 函數,且y=f(x)的最大值為2,其圖象相鄰兩對稱軸的距離為2,并過點(1,2).
函數,且y=f(x)的最大值為2,其圖象相鄰兩對稱軸的距離為2,并過點(1,2).
(1)求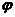 ;
;
(2)計算f(1)+f(2)+… +f(2 008).
(18)(本小題滿分12分)
設函數f(x)=ax-(a+1)ln(x+1),其中a -1,求f(x)的單調區間。
-1,求f(x)的單調區間。
(19)(本小題滿分12分)
如圖ABC-A1B1C1,已知平面平行于三棱錐V-A1B1C1的底面ABC,等邊∆ AB1C所在的平面與底面ABC垂直,且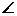 ABC=90°,設AC=2a,BC=a.
ABC=90°,設AC=2a,BC=a.
(1)求證直線B1C1是異面直線與A1C1的公垂線;
(2)求點A到平面VBC的距離;
(3)求二面角A-VB-C的大小.
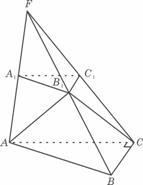
(19題圖)
(20) (本小題滿分12分)
袋中裝著標有數學1,2,3,4,5的小球各2個,從袋中任取3個小球,按3個小球上最大數字的9倍計分,每個小球被取出的可能性都相等,用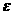 表示取出的3個小球上的最大數字,求:
表示取出的3個小球上的最大數字,求:
(1)取出的3個小球上的數字互不相同的概率;
(2)隨機變量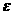 的概率分布和數學期望;
的概率分布和數學期望;
(3)計分介于20分到40分之間的概率.
(21)(本小題滿分12分)
雙曲線C與橢圓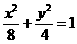 有相同的熱點,直線y=
有相同的熱點,直線y=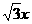 為C的一條漸近線.
為C的一條漸近線.
(1) 求雙曲線C的方程;
(2)
過點P(0,4)的直線l,求雙曲線C于A,B兩點,交x軸于Q點(Q點與C的頂點不重合).當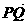 =
=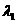
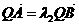 ,且
,且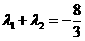 時,求Q點的坐標.
時,求Q點的坐標.
(22)(本小題滿分14分)
已知a1=2,點(an,an+1)在函數f(x)=x2+2x的圖象上,其中=1,2,3,…
(1) 證明數列{lg(1+an)}是等比數列;
(2) 設Tn=(1+a1) (1+a2) …(1+an),求Tn及數列{an}的通項;
(3)
記bn=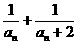 ,求{bn}數列的前項和Sn,并證明Sn+
,求{bn}數列的前項和Sn,并證明Sn+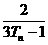 =1.
=1.
(13)若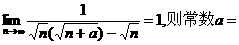 .
.
(14)已知拋物線y2=4x,過點P(4,0)的直線與拋物線相交于A(x1,y1),B(x2,y2)兩點,則y12+y22的最小值是 .
(15)如圖,已知正三棱柱ABC-A1B1C1的所有棱長都相等,D是A1C1的 中點,則直線AD 與平面B1DC所成角的正弦值為 .
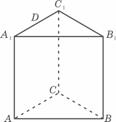
(15題圖)
(16)下列四個命題中,真命題的序號有 (寫出所有真命題的序號).
①將函數y=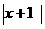 的圖象按向量y=(-1,0)平移,得到的圖象對應的函數表達式為y=
的圖象按向量y=(-1,0)平移,得到的圖象對應的函數表達式為y=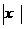
②圓x2+y2+4x-2y+1=0與直線y=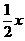 相交,所得弦長為2
相交,所得弦長為2
③若sin( +
+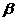 )=
)=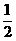 ,則sin(
,則sin( +
+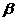 )=
)=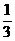 ,則tan
,則tan cot
cot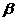 =5
=5
④如圖,已知正方體ABCD- A1B1C1D1,P為底面ABCD內一動點,P到平面AA1D1D的距離與到直線CC1的距離相等,則P點的軌跡是拋物線的一部分.
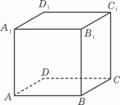
(16題圖)
(1)定義集合運算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},設集合A={0,1},B={2,3},則集合A⊙B的所有元素之和為
(A)0 (B)6 (C)12 (D)18
(2)函數y=1+ax(0<a<1)的反函數的圖象大致是

(A) (B) (C) (D)
(3)設f(x)=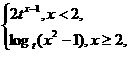
 則不等式f(x)>2的解集為
則不等式f(x)>2的解集為
(A)(1,2)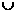 (3,+∞)
(B)(
(3,+∞)
(B)(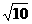 ,+∞)
,+∞)
(C)(1,2)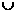 (
(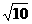 ,+∞) (D)(1,2)
,+∞) (D)(1,2)
(4)在△ABC中,角A、B、C的對邊分別為a、b、c,A=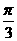 ,a=
,a=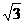 ,b=1,則c=
,b=1,則c=
(A)
1
(B)2 (C)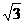 -1
(D)
-1
(D)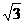
(5)設向量a=(1,2),b=(-1,1),c=(-1,-2),若表示向量4a,4b-2c,2(a-c),d的有向線段首尾相連能構成四邊形,則向量d為
(A)(2,6) (B)(-2,6) (C)(2,-6) (D)(-2,-6)
(6)已知定義在R上的奇函數f(x)滿足f(x+2)=-f(x),則,f(6)的值為
(A)-1 (B) 0 (C) 1 (D)2
(7)在給定橢圓中,過焦點且垂直于長軸的弦長為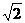 ,焦點到相應準線的距離為1,則該橢圓的離心率為
,焦點到相應準線的距離為1,則該橢圓的離心率為
(A)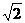 (B)
(B)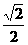 (C)
(C) 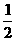 (D)
(D)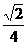
(8)設p:x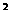 -x-20>0,q:
-x-20>0,q: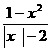 <0,則p是q的
<0,則p是q的
(A)充分不必要條件 (B)必要不充分條件
(C)充要條件 (D)既不充分也不必要條件
(9)已知集合A={5},B={1,2},C={1,3,4},從這三個集合中各取一個元素構成空間直角坐標系中點的坐標,則確定的不同點的個數為
(A)33 (B) 34 (C) 35 (D)36
(10)已知 的展開式中第三項與第五項的系數之比為-
的展開式中第三項與第五項的系數之比為-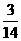 ,其中i
,其中i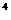 =-1,則展開式中常數項是
=-1,則展開式中常數項是
(A)-45i (B) 45i (C) -45 (D)45
(11)某公司招收男職員x名,女職員y名,x和y須滿足約束條件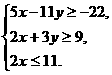 則z=10x+10y的最大值是
則z=10x+10y的最大值是
(A)80 (B) 85 (C) 90 (D)95
(12)如圖,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E為AB的中點,將△ADE與△BEC分別沿ED、EC向上折起,使A、B重合于點P,則P-DCE三棱錐的外接球的體積為
(A) (B)
(B)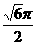 (C)
(C)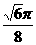 (D)
(D)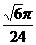
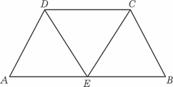
(12題圖)
絕密★啟用前
普通高等學校招生全國統一考試
理科數學(必修+選修II)
(17)(本小題滿分12分)
在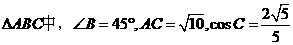 ,求
,求
(1)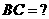
(2)若點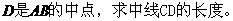
(18)(本小題滿分12分)
設等比數列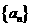 的前n項和為
的前n項和為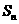 ,
,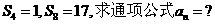
(19)(本小題滿分12分)
某批產品成箱包裝,每箱5件,一用戶在購進該批產品前先取出3箱,再從每箱中任意出取2件產品進行檢驗。設取出的第一、二、三箱中分別有0件、1件、2件二等品,其余為一等品。
(I)求取6件產品中有1件產品是二等品的概率。
(II)若抽檢的6件產品中有2件或2件以上二等品,用戶就拒絕購買這批產品,求這批產品被用戶拒絕的概率。
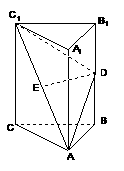 (20)(本小題12分)
(20)(本小題12分)
如圖,在直三棱柱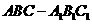 中,
中,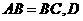 、
、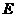 分別為
分別為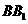 、
、 的中點。
的中點。
(I)證明:ED為異面直線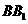 與
與 的公垂線;
的公垂線;
(II)設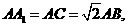 求二面角
求二面角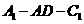 的大小
的大小
(21)(本小題滿分為14分)
設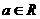 ,函數
,函數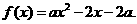 若
若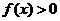 的解集為A,
的解集為A,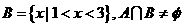 ,求實數
,求實數 的取值范圍。
的取值范圍。
(22)(本小題滿分12分)
已知拋物線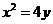 的焦點為F,A、B是拋物線上的兩動點,且
的焦點為F,A、B是拋物線上的兩動點,且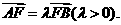 過A、B兩點分別作拋物線的切線,設其交點為M。
過A、B兩點分別作拋物線的切線,設其交點為M。
(I)證明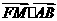 為定值;
為定值;
(II)設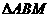 的面積為S,寫出
的面積為S,寫出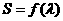 的表達式,并求S的最小值。
的表達式,并求S的最小值。
普通高等學校招生全國統一考試(全國II卷)
(13)在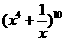 的展開式中常數項是_____。(用數字作答)
的展開式中常數項是_____。(用數字作答)
(14)圓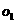 是以
是以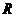 為半徑的球
為半徑的球 的小圓,若圓
的小圓,若圓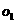 的面積
的面積 和球
和球 的表面積
的表面積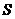 的比為
的比為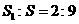 ,則圓心
,則圓心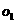 到球心
到球心 的距離與球半徑的比
的距離與球半徑的比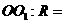 _____。
_____。
(15)過點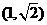 的直線
的直線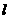 將圓
將圓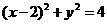 分成兩段弧,當劣弧所對的圓心角最小時,直線
分成兩段弧,當劣弧所對的圓心角最小時,直線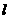 的斜率
的斜率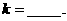
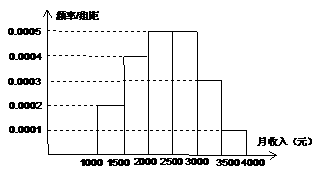 (16)一個社會調查機構就某地居民的月收入調查了10000人,并根據所得數據畫了樣本的頻率分布直方圖(如下圖)。為了分析居民的收入與年齡、學歷、職業等方面的關系,要從這10000人中再用分層抽樣方法抽出100人作進一步調查,則在
(16)一個社會調查機構就某地居民的月收入調查了10000人,并根據所得數據畫了樣本的頻率分布直方圖(如下圖)。為了分析居民的收入與年齡、學歷、職業等方面的關系,要從這10000人中再用分層抽樣方法抽出100人作進一步調查,則在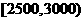 (元)月收入段應抽出_____人。
(元)月收入段應抽出_____人。
(1)已知向量 =(4,2),向量
=(4,2),向量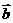 =(
=(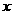 ,3),且
,3),且 //
//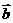 ,則
,則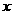 =( )
=( )
(A)9 (B)6 (C)5 (D)3
(2)已知集合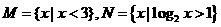 ,則
,則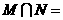 ( )
( )
(A)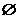 (B)
(B)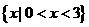 (C)
(C) (D)
(D)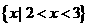
(3)函數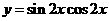 的最小正周期是( )
的最小正周期是( )
(A)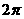 (B)
(B)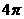 (C)
(C)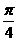 (D)
(D)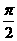
(4)如果函數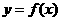 的圖像與函數
的圖像與函數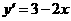 的圖像關于坐標原點對稱,則
的圖像關于坐標原點對稱,則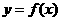 的表達式為( )
的表達式為( )
(A)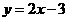 (B)
(B)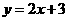 (C)
(C)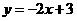 (D)
(D)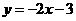
(5)已知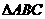 的頂點B、C在橢圓
的頂點B、C在橢圓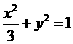 上,頂點A是橢圓的一個焦點,且橢圓的另外一個焦點在BC邊上,則
上,頂點A是橢圓的一個焦點,且橢圓的另外一個焦點在BC邊上,則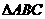 的周長是( )
的周長是( )
(A) (B)6 (C)
(B)6 (C)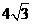 (D)12
(D)12
(6)已知等差數列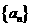 中,
中,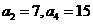 ,則前10項的和
,則前10項的和 =( )
=( )
(A)100 (B)210 (C)380 (D)400
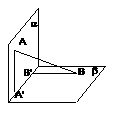 (7)如圖,平面
(7)如圖,平面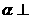 平面
平面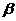 ,
,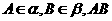 與兩平面
與兩平面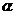 、
、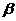 所成的角分別為
所成的角分別為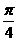 和
和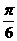 。過A、B分別作兩平面交線的垂線,垂足為
。過A、B分別作兩平面交線的垂線,垂足為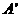 、
、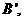 若AB=12,則
若AB=12,則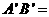 ( )
( )
(A)4 (B)6 (C)8 (D)9
(8)已知函數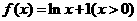 ,則
,則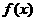 的反函數為( )
的反函數為( )
(A)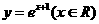 (B)
(B)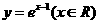
(C) (D)
(D)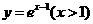
(9)已知雙曲線 的一條漸近線方程為
的一條漸近線方程為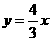 ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )
(A)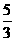 (B)
(B)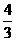 (C)
(C)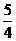 (D)
(D)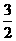
(10)若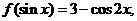 則
則 ( )
( )
(A) (B)
(B)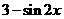 (C)
(C) (D)
(D)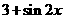
(11)過點(-1,0)作拋物線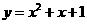 的切線,則其中一條切線為( )
的切線,則其中一條切線為( )
(A)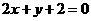 (B)
(B) (C)
(C)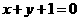 (D)
(D)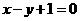
(12)5名志愿者分到3所學校支教,每個學校至少去一名志愿者,則不同的分派方法共有( )
(A)150種 (B)180種 (C)200種 (D)280種
第Ⅱ卷
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com