
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程是:
的參數方程是: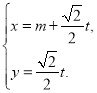 (
(![]() 是參數).以原點
是參數).以原點![]() 為極點,x軸的正半軸為極軸建立極坐標系,曲線
為極點,x軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,試求實數
,試求實數![]() 值;
值;
(2)設![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】某工廠為提高生產效率,需引進一條新的生產線投入生產,現有兩條生產線可供選擇,生產線①:有A,B兩道獨立運行的生產工序,且兩道工序出現故障的概率依次是0.01,0.05.若兩道工序都沒有出現故障,則生產成本為16萬元;若A工序出現故障,則生產成本增加2萬元;若B工序出現故障,則生產成本增加3萬元;若A,B兩道工序都出現故障,則生產成本增加5萬元.生產線②:有a,b兩道獨立運行的生產工序,且兩道工序出現故障的概率依次是0.04,0.02.若兩道工序都沒有出現故障,則生產成本為15萬元;若a工序出現故障,則生產成本增加8萬元;若b工序出現故障,則生產成本增加5萬元;若a,b兩道工序都出現故障,則生產成本增加13萬元.
(1)若選擇生產線②,求生產成本恰好為20萬元的概率;
(2)為最大限度節約生產成本,你會給工廠建議選擇哪條生產線?請說明理由.
查看答案和解析>>
科目: 來源: 題型:
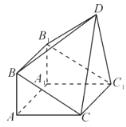
【題目】如圖,由直三棱柱![]() 和四棱錐
和四棱錐![]() 構成的幾何體中,
構成的幾何體中,![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)求證:![]() ;
;
(2)在線段![]() 上(含端點)是否存在點P,使直線
上(含端點)是否存在點P,使直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?若存在,求
?若存在,求![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目: 來源: 題型:
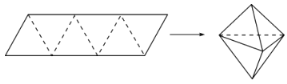
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽粒,古稱角黍,是端午節大家都會品嘗的食品.如圖,平行四邊形形狀的紙片是由六個邊長為2的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為_________;若該六面體內有一球,當該球體積最大時,球的表面積是__________.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)若曲線![]() 與曲線
與曲線![]() 在公共點處有共同的切線,求實數
在公共點處有共同的切線,求實數![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,試問函數![]() 是否有零點?如果有,求出該零點;若沒有,請說明理由.
是否有零點?如果有,求出該零點;若沒有,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
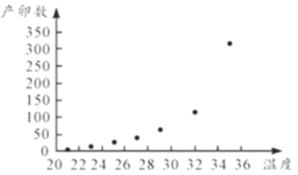
【題目】從![]() 年底開始,非洲東部的肯尼亞等國家爆發出了一場嚴重的蝗蟲災情.目前,蝗蟲已抵達烏干達和坦桑尼亞,并向西亞和南亞等地區蔓延.蝗蟲危害大,主要危害禾本科植物,能對農作物造成嚴重傷害,每只蝗蟲的平均產卵數
年底開始,非洲東部的肯尼亞等國家爆發出了一場嚴重的蝗蟲災情.目前,蝗蟲已抵達烏干達和坦桑尼亞,并向西亞和南亞等地區蔓延.蝗蟲危害大,主要危害禾本科植物,能對農作物造成嚴重傷害,每只蝗蟲的平均產卵數![]() 和平均溫度
和平均溫度![]() 有關,現收集了以往某地的
有關,現收集了以往某地的![]() 組數據,得到下面的散點圖及一些統計量的值.
組數據,得到下面的散點圖及一些統計量的值.
平均溫度 |
|
|
|
|
|
|
|
平均產卵數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() (其中
(其中![]() 為自然對數的底數)哪一個更適宜作為平均產卵數
為自然對數的底數)哪一個更適宜作為平均產卵數![]() 關于平均溫度
關于平均溫度![]() 的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出
的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出![]() 關于
關于![]() 的回歸方程.(結果精確到小數點后第三位)
的回歸方程.(結果精確到小數點后第三位)
(2)根據以往統計,該地每年平均溫度達到![]() 以上時蝗蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治,記該地每年平均溫度達到
以上時蝗蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治,記該地每年平均溫度達到![]() 以上的概率為
以上的概率為![]() .
.
①記該地今后![]() 年中,恰好需要
年中,恰好需要![]() 次人工防治的概率為
次人工防治的概率為![]() ,求
,求![]() 取得最大值時相應的概率
取得最大值時相應的概率![]() ;
;
②根據①中的結論,當![]() 取最大值時,記該地今后
取最大值時,記該地今后![]() 年中,需要人工防治的次數為
年中,需要人工防治的次數為![]() ,求
,求![]() 的數學期望和方差.
的數學期望和方差.
附:對于一組數據![]() 、
、![]() 、
、![]() 、
、![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為: ,
,![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,點E是BC的中點.將△ABD沿BD折起,使AB⊥AC,連接AE,AC,DE,得到三棱錐A-BCD.
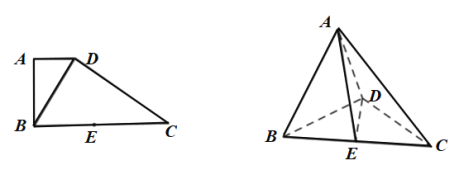
(1)求證:平面ABD⊥平面BCD
(2)若AD=1,二面角C-AB-D的余弦值為![]() ,求二面角B-AD-E的正弦值.
,求二面角B-AD-E的正弦值.
查看答案和解析>>
科目: 來源: 題型:
【題目】對n個不同的實數a1,a2,…,an可得n!個不同的排列,每個排列為一行寫成一個n!行的數陣.對第i行ai1,ai2,…,ain,記bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3…,n!.例如用1,2,3可得數陣如圖,對于此數陣中每一列各數之和都是12,所以bl+b2+…b6=-12+2×12-3×12=-24.那么,在用1,2,3,4,5形成的數陣中,b1+b2+…b120等于( )

A.-3600B.-1800C.-1080D.-720
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com