
【題目】在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,點E是BC的中點.將△ABD沿BD折起,使AB⊥AC,連接AE,AC,DE,得到三棱錐A-BCD.
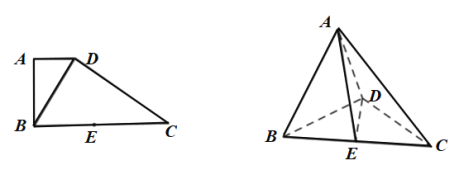
(1)求證:平面ABD⊥平面BCD
(2)若AD=1,二面角C-AB-D的余弦值為![]() ,求二面角B-AD-E的正弦值.
,求二面角B-AD-E的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)由AB⊥AC和AB⊥AD,可得AB⊥平面ADC,所以AB⊥CD,而BD⊥DC,所以CD⊥平面ADB,從而可證得平面ABD⊥平面BCD;
(2)由AB⊥平面ADC,可知二面角C-AB-D的平面角為∠CAD,由二面角C-AB-D的余弦值為![]() ,解出AB,建立空間直角坐標系D-xyz,求出平面ABD的法向量,平面AED的法向量,即可得二面角B-AD-E的正弦值
,解出AB,建立空間直角坐標系D-xyz,求出平面ABD的法向量,平面AED的法向量,即可得二面角B-AD-E的正弦值
(1)證明:因為直角梯形ABCD中,AD∥BC,AB⊥BC,
所以AB⊥AD,
因為AB⊥AC,![]() ,所以AB⊥平面ADC,
,所以AB⊥平面ADC,
所以AB⊥CD,
因為BD⊥DC, ![]() ,
,
所以CD⊥平面ADB,
因為CD在平面BCD內,
所以平面ABD⊥平面BCD
(2)由(1)知AB⊥平面ADC,
所以二面角C-AB-D的平面角為∠CAD,
因為CD⊥平面ADB,所以AD⊥CD,
所以![]() ,得
,得![]() ,所以
,所以![]() ,
,
設![]() ,則
,則![]() ,
,
由題意可知![]()
![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() ,
,
如圖所示,建立空間直角坐標系D-xyz,則
![]() ,
,
所以![]() ,
,
因為CD⊥平面ADB,所以令平面ADB的法向量為![]() ,
,
設平面AED的法向量為![]() ,則
,則
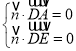 ,即
,即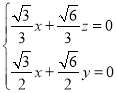 ,
,
取![]() ,則
,則![]() ,
,
設二面角B-AD-E的平面角為![]() ,
,
則![]() ,
,
所以![]() ,
,
所以二面角B-AD-E的正弦值為![]() ,
,


科目:高中數學 來源: 題型:
【題目】垃圾分類是對垃圾進行有效處置的一種科學管理方法.太原市為推進這項工作的實施,開展了“垃圾分類進小區”的評比活動.現有甲、乙兩個小區采取不同的宣傳與倡導方式對各自小區居民進行了有關垃圾分類知識的培訓,并參加了評比活動,評委會隨機從兩個小區各選出20戶家庭進行評比打分,每戶成績滿分為100分,評分后得到如下莖葉圖.
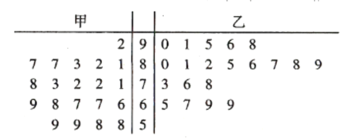
(1)依莖葉圖判斷哪個小區的平均分高?
(2)現從甲小區不低于80分的家庭中隨機抽取兩戶,求分數為87的家庭至少有一戶被抽中的概率;
(3)如果規定分數不低于85分的家庭為優秀,請填寫下面的![]() 列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為得分是否優秀與小區宣傳培訓方式有關?”
列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為得分是否優秀與小區宣傳培訓方式有關?”
甲 | 乙 | 合計 | |
優秀 |
|
| |
不優秀 |
|
| |
合計 |
參考公式和數據: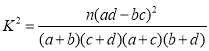 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年1月1日,我國開始施行《個人所得稅專項附加扣除操作辦法》,附加扣除的專項包括子女教育、繼續教育、大病醫療、住房貨款利息、住房租金、贍養老人.某單位有老年員工140人,中年員工180人,青年員工80人,現采用分層抽樣的方法,從該單位員工中抽取20人,調查享受個人所得稅專項附加扣除的情況,并按照員工類別進行各專項人數匯總,數據統計如下:
員工\人數\專項 | 子女教育 | 繼續教育 | 大病醫療 | 住房貸款利息 | 住房租金 | 贍養老人 |
老員工 | 4 | 0 | 2 | 2 | 0 | 3 |
中年員工 | 8 | 2 | 1 | 5 | 1 | 8 |
青年員工 | 1 | 2 | 0 | 1 | 2 | 1 |
(Ⅰ)在抽取的20人中,老年員工、中年員工、青年員工各有多少人;
(Ⅱ)從上表享受住房貨款利息專項扣除的員工中隨機選取2人,求選取2人都是中年員工的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是無窮數列,若存在正整數k,使得對任意
是無窮數列,若存在正整數k,使得對任意![]() ,均有
,均有![]() ,則稱
,則稱![]() 是間隔遞增數列,k是
是間隔遞增數列,k是![]() 的間隔數,下列說法正確的是( )
的間隔數,下列說法正確的是( )
A.公比大于1的等比數列一定是間隔遞增數列
B.已知![]() ,則
,則![]() 是間隔遞增數列
是間隔遞增數列
C.已知![]() ,則
,則![]() 是間隔遞增數列且最小間隔數是2
是間隔遞增數列且最小間隔數是2
D.已知![]() ,若
,若![]() 是間隔遞增數列且最小間隔數是3,則
是間隔遞增數列且最小間隔數是3,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
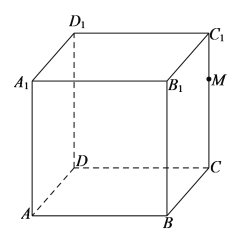
【題目】已知正方體![]() 棱長為
棱長為![]() ,如圖,
,如圖,![]() 為
為![]() 上的動點,
上的動點,![]() 平面
平面![]() .下面說法正確的是( )
.下面說法正確的是( )
A.直線![]() 與平面
與平面![]() 所成角的正弦值范圍為
所成角的正弦值范圍為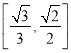
B.點![]() 與點
與點![]() 重合時,平面
重合時,平面![]() 截正方體所得的截面,其面積越大,周長就越大
截正方體所得的截面,其面積越大,周長就越大
C.點![]() 為
為![]() 的中點時,若平面
的中點時,若平面![]() 經過點
經過點![]() ,則平面
,則平面![]() 截正方體所得截面圖形是等腰梯形
截正方體所得截面圖形是等腰梯形
D.己知![]() 為
為![]() 中點,當
中點,當![]() 的和最小時,
的和最小時,![]() 為
為![]() 的中點
的中點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,由直三棱柱![]() 和四棱錐
和四棱錐![]() 構成的幾何體中,
構成的幾何體中,![]() ,平面
,平面![]() 平面
平面![]() .
.
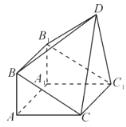
(1)求證:![]() ;
;
(2)在線段![]() 上(含端點)是否存在點P,使直線
上(含端點)是否存在點P,使直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?若存在,求
?若存在,求![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是坐標系的原點,
是坐標系的原點,![]() 是拋物線
是拋物線![]() 的焦點,過點
的焦點,過點![]() 的直線交拋物線于
的直線交拋物線于![]() ,
,![]() 兩點,弦
兩點,弦![]() 的中點為
的中點為![]() ,
,![]() 的重心為
的重心為![]() .
.
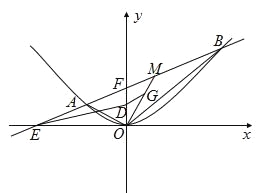
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)設(1)中的軌跡與![]() 軸的交點為
軸的交點為![]() ,當直線
,當直線![]() 與
與![]() 軸相交時,令交點為
軸相交時,令交點為![]() ,求四邊形
,求四邊形![]() 的面積最小時直線
的面積最小時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】干支紀年法是中國歷法上自古以來就一直使用的紀年方法、干支是天干和地支的總稱,甲、乙、丙、丁、戊、己、庚、辛、壬、癸為天干:子、丑、寅、卯、辰、已、午、未,申、西、戌、亥為地支.把十天干和十二地支依次相配,如甲對子、乙對丑、丙對寅、…癸對寅,其中天干比地支少兩位,所以天干先循環,甲對戊、乙對亥、…接下來地支循環,丙對子、丁對丑、.,以此用來紀年,今年2020年是庚子年,那么中華人民共和國建國100周年即2049年是( )
A.戊辰年B.己巳年C.庚午年D.庚子年
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com