
【題目】如圖,由直三棱柱![]() 和四棱錐
和四棱錐![]() 構成的幾何體中,
構成的幾何體中,![]() ,平面
,平面![]() 平面
平面![]() .
.
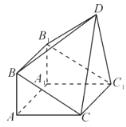
(1)求證:![]() ;
;
(2)在線段![]() 上(含端點)是否存在點P,使直線
上(含端點)是否存在點P,使直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?若存在,求
?若存在,求![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
【答案】(1)證明見解析;(2)存在;![]() .
.
【解析】
(1)根據題意可知![]() ,然后根據面面垂直的性質定理可知
,然后根據面面垂直的性質定理可知![]() 平面
平面![]() ,進一步可得結果.
,進一步可得結果.
(2)建立空間直角坐標系,假設![]() 計算平面
計算平面![]() 的一個法向量
的一個法向量![]() ,以及
,以及![]() ,然后根據
,然后根據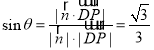 ,計算可得
,計算可得![]() .
.
(1)證明:直三棱柱![]() 中,
中,![]() ,
,
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)假設線段![]() 上(含端點)存在點P,
上(含端點)存在點P,
使直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ,
,
以A為原點,![]() 為x軸,
為x軸,![]() 為y軸,
為y軸,![]() 為z軸,
為z軸,
建立空間直角坐標系,如圖
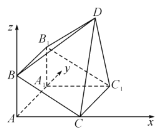
則![]() ,
,
設![]() ,
,
則![]() ,
,![]() ,
,
所以![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則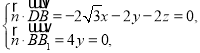 取
取![]() ,得
,得![]() ,
,
因為直線![]() 與平面
與平面![]() 所成的角正弦值為
所成的角正弦值為![]() ,
,
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
所以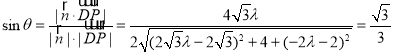 ,
,
解得![]() ,或
,或![]() (舍)
(舍)
所以在線段![]() 上(含端點)存在點P,
上(含端點)存在點P,
使直線![]() 與平面
與平面![]() 所成的角正弦值為
所成的角正弦值為![]() ,
,
解得![]() .
.


科目:高中數學 來源: 題型:
【題目】函數![]() (
(![]() ,
,![]() )的部分圖象如圖所示,則下列結論正確的是( )
)的部分圖象如圖所示,則下列結論正確的是( )
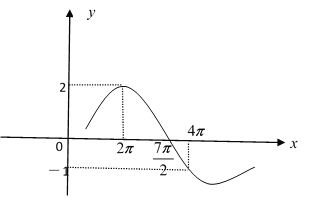
A.![]()
B.若把函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位,則所得函數是奇函數
個單位,則所得函數是奇函數
C.若把![]() 的橫坐標縮短為原來的
的橫坐標縮短為原來的![]() 倍,縱坐標不變,得到的函數在
倍,縱坐標不變,得到的函數在![]() 上是增函數
上是增函數
D.![]() ,若
,若![]() 恒成立,則
恒成立,則![]() 的最小值為
的最小值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“支付寶捐步”已經成為當下最熱門的健身方式,為了了解是否使用支付寶捐步與年齡有關,研究人員隨機抽取了5000名使用支付寶的人員進行調查,所得情況如下表所示:
50歲以上 | 50歲以下 | |
使用支付寶捐步 | 1000 | 1000 |
不使用支付寶捐步 | 2500 | 500 |
(1)由上表數據,能否有99.9%的把握認為是否使用支付寶捐步與年齡有關?
(2)55歲的老王在了解了捐步功能以后開啟了自己的捐步計劃,可知其在捐步的前5天,捐步的步數與天數呈線性相關.
第x天 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
步數 | 4000 | 4200 | 4300 | 5000 | 5500 |
(i)根據上表數據,建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(ii)記由(i)中回歸方程得到的預測步數為![]() ,若從5天中任取3天,記
,若從5天中任取3天,記![]() 的天數為X,求X的分布列以及數學期望.
的天數為X,求X的分布列以及數學期望.
附參考公式與數據: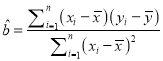 ,
,![]() ;K2=
;K2=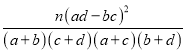 ;
;
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面上一動點A的坐標為![]() .
.
(1)求點A的軌跡E的方程;
(2)點B在軌跡E上,且縱坐標為![]() .
.
(i)證明直線AB過定點,并求出定點坐標;
(ii)分別以A,B為圓心作與直線![]() 相切的圓,兩圓公共弦的中點為H,在平面內是否存在定點P,使得
相切的圓,兩圓公共弦的中點為H,在平面內是否存在定點P,使得![]() 為定值?若存在,求出點P坐標;若不存在,請說明理由.
為定值?若存在,求出點P坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,點E是BC的中點.將△ABD沿BD折起,使AB⊥AC,連接AE,AC,DE,得到三棱錐A-BCD.
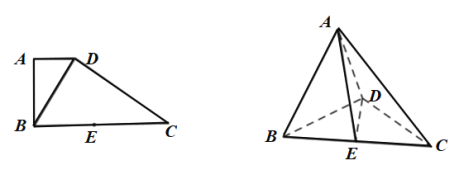
(1)求證:平面ABD⊥平面BCD
(2)若AD=1,二面角C-AB-D的余弦值為![]() ,求二面角B-AD-E的正弦值.
,求二面角B-AD-E的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為平面直角坐標系的原點,極軸為
,以極點為平面直角坐標系的原點,極軸為![]() 軸的正半軸,且取相等的單位長度,建立平面直角坐標系,直線
軸的正半軸,且取相等的單位長度,建立平面直角坐標系,直線![]() 的參數方程是
的參數方程是 (
(![]() 是參數),設點
是參數),設點![]() .
.
(Ⅰ)將曲線![]() 的極坐標方程化為直角坐標方程,將直線
的極坐標方程化為直角坐標方程,將直線![]() 的參數方程化為普通方程;
的參數方程化為普通方程;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且橢圓上一點
,且橢圓上一點![]() 的坐標為
的坐標為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以線段
兩點,且以線段![]() 為直徑的圓過橢圓的右頂點
為直徑的圓過橢圓的右頂點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是圓
是圓![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 軸于點
軸于點![]() ,延長
,延長![]() 到點
到點![]() ,使
,使![]() .
.
(1)求點M的軌跡E的方程;
(2)過點![]() 作圓O的切線l,交(1)中曲線E于
作圓O的切線l,交(1)中曲線E于![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com