
分析 設f(α)=$\frac{sinα}{|sinα|}$+$\frac{cosα}{|cosα|}$+$\frac{tanα}{|tanα|}$,當α∈(0,$\frac{π}{2}$)時,f(α)=3;當α∈($\frac{π}{2}$,π)時,f(α)=-1;當α∈($π,\frac{3π}{2}$)時,f(α)=-1;當α∈(π,2π)時,f(α)=-1.由此能求出該數是方程$\frac{sinα}{|sinα|}$+$\frac{cosα}{|cosα|}$+$\frac{tanα}{|tanα|}$=-1的解的概率.
解答 解:∵在區間[0,2π]上任取一個實數α,
設f(α)=$\frac{sinα}{|sinα|}$+$\frac{cosα}{|cosα|}$+$\frac{tanα}{|tanα|}$,
∴當α∈(0,$\frac{π}{2}$)時,f(α)=1+1+1=3;
當α∈($\frac{π}{2}$,π)時,f(α)=1-1-1=-1;
當α∈($π,\frac{3π}{2}$)時,f(α)=-1-1+1=-1;
當α∈(π,2π)時,f(α)=-1+1-1=-1.
∴該數是方程$\frac{sinα}{|sinα|}$+$\frac{cosα}{|cosα|}$+$\frac{tanα}{|tanα|}$=-1的解的概率p=$\frac{2π-\frac{π}{2}}{2π-0}$=$\frac{3}{4}$.
故答案為:$\frac{3}{4}$.
點評 本題考查概率的求法,是基礎題,解題時要認真審題,注意三角函數性質、幾何概型的合理運用.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | cos10° | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -sin10° |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
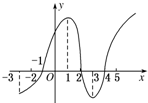 如圖所示是y=f(x)的導數圖象,則下列判斷中正確結論的序號是②④.
如圖所示是y=f(x)的導數圖象,則下列判斷中正確結論的序號是②④.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 棱長為1的正方體的內切球的表面積為4π | |
| B. | 三條平行直線最多確定三個平面 | |
| C. | 正方體ABCD-A1B1C1D1中,AB與C1D1異面 | |
| D. | 若平面α⊥平面β,平面β⊥平面γ,則平面α∥平面γ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com