
分析 ①,兩個函數的定義域和對應法則相同;
②,函數y=x3的值域為R,函數y=3x的值域為(0,+∞);
③,函數y=$\frac{1}{2$+$\frac{1}{{{2^x}-1}}$與y=-$\frac{1}{x}$均滿足定義域關于原點對稱和f(x)+f(-x)=0;
④,函數y=(x-1)2的增區間是 (1,+∞).
解答 解:對于①,兩個函數的定義域和對應法則相同,所以是同一函數,故正確;
對于②,函數y=x3的值域為R,函數y=3x的值域為(0,+∞),故錯;
對于③,函數y=$\frac{1}{2$+$\frac{1}{{{2^x}-1}}$與y=-$\frac{1}{x}$均滿足定義域關于原點對稱和f(x)+f(-x)=0,所以都是奇函數,故正確;
對于④,函數y=(x-1)2的增區間是 (1,+∞),故錯.
故答案為:①③.
點評 本題考查了命題真假判定,涉及到了函數的概念機性質,屬于基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
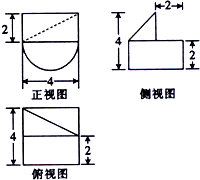
| A. | $\frac{16}{3}$+8π | B. | $\frac{32}{3}$+8π | C. | 16+8π | D. | $\frac{16}{3}$+16π |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-2,-1} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com