
分析 (1)由題意可設橢圓的標準方程為:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),可得$\frac{c}{a}=\frac{\sqrt{6}}{3}$,a=$\sqrt{5}$,a2=b2+c2,解出可得橢圓的方程.直線斜率不存在時顯然不成立,設直線AB:y=k(x+1),將AB:y=k(x+1)代入橢圓的方程,消去y整理得(3k2+1)x2+6k2x+3k2-5=0,由線段AB的中點的橫坐標為$-\frac{1}{2}$,解得k,即可得出.
(2)假設在x軸上存在點M(m,0),使得MA•MB為常數,
①當直線AB與x軸不垂直時,利用根與系數的關系與數量積運算性質可得$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x1-m)(x2-m)+y1y2,即可得出.
解答 解:(1)由題意可設橢圓的標準方程為:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
∴$\frac{c}{a}=\frac{\sqrt{6}}{3}$,a=$\sqrt{5}$,a2=b2+c2,
解得a=$\sqrt{5}$,c=$\frac{\sqrt{30}}{3}$,b2=$\frac{5}{3}$.
∴橢圓的方程為x2+3y2=5,
直線斜率不存在時顯然不成立,設直線AB:y=k(x+1),
將AB:y=k(x+1)代入橢圓的方程,消去y整理得(3k2+1)x2+6k2x+3k2-5=0,
設A(x1,y1),B(x2,y2),則$\left\{{\begin{array}{l}{△=36{k^4}-4({3{k^2}+1})({3{k^2}-5})>0}\\{{x_1}+{x_2}=-\frac{{6{k^2}}}{{3{k^2}+1}}}\end{array}}\right.$,
∵線段AB的中點的橫坐標為$-\frac{1}{2}$,解得$k=±\frac{{\sqrt{3}}}{3}$,
∴直線AB的方程為$x±\sqrt{3}y+1=0$.
(2)假設在x軸上存在點M(m,0),使得MA•MB為常數,
①當直線AB與x軸不垂直時,由(1)知${x_1}+{x_2}=-\frac{{6{k^2}}}{{3{k^2}+1}},{x_1}•{x_2}=\frac{{3{k^2}-5}}{{3{k^2}+1}}$,
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x1-m)(x2-m)+y1y2=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2=${m^2}+2m-\frac{1}{3}-\frac{6m+14}{{3({3{k^2}+1})}}$,
∵$\overrightarrow{MA}$•$\overrightarrow{MB}$是與k無關的常數,從而有$6m+14=0,m=-\frac{7}{3}$,
此時$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\frac{4}{9}$.
②當直線AB與x軸垂直時,此時結論成立,
綜上可知,在x軸上存在定點$M({-\frac{7}{3},0})$,使$MA•MB=\frac{4}{9}$,為常數.
點評 本題考查了橢圓的標準方程及其性質、向量數量積運算性質、一元二次方程的根與系數的關系、中點坐標公式,考查了推理能力與計算能力,屬于難題.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
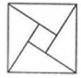 2002年在北京召開的國際數學家大會,會標是以我國古代數學家趙爽的弦圖為基礎設計的.弦圖是由四個全等直角三角形與一個小正方形拼成的一個大正方形(如圖).如果小正方形的面積為1,大正方形的面積為25,直角三角形中較小的銳角為θ,那么sin2θ的值為( )
2002年在北京召開的國際數學家大會,會標是以我國古代數學家趙爽的弦圖為基礎設計的.弦圖是由四個全等直角三角形與一個小正方形拼成的一個大正方形(如圖).如果小正方形的面積為1,大正方形的面積為25,直角三角形中較小的銳角為θ,那么sin2θ的值為( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{23}{24}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({\frac{1}{e},e})$ | B. | $({\frac{1}{2e},\frac{1}{e}})$ | C. | $({-∞,\frac{1}{2e}})$ | D. | $({\frac{1}{2e},+∞})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | -4 | C. | 0 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com