Question

5．在平面直角坐標系xOy中，拋物線y²=4x的焦點為F，準線交x軸于點H，過H作直線l交拋物線于A，B兩點，且|BF|=2|AF|，則△ABF的面積為$\sqrt{2}$．

Answer 1

分析 過A，B兩點作準線的垂線，垂足分別為A₁，B₁，運用拋物線的定義，結合條件可得AO是△BHF的中位線，運用中位線定理，可得A的坐標，再由三角形的面積公式，計算即可得到所求值．

解答 解：過A，B兩點作準線的垂線，垂足分別為A₁，B₁，
易知|AF=AA₁|，|BF|=|BB₁|，
∵|BF|=2|AF|，∴|BB₁|=2|AA₁|，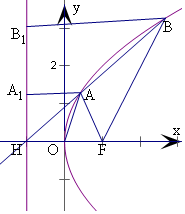
∴A為HB的中點，又O是HF的中點，
∴AO是△BHF的中位線，∴|AO|=$\frac{1}{2}$|BF|=|AF|，
而拋物線的焦點F（1，0），
∴x_A=$\frac{1}{2}$，
∴y_A²=4×$\frac{1}{2}$=2，
y_A=±$\sqrt{2}$，
∴A（$\frac{1}{2}$，±$\sqrt{2}$），
∵A為HB的中點，O是HF的中點，
∴S_△ABF=S_△AHF=$\frac{1}{2}$×$\sqrt{2}$×2=$\sqrt{2}$．
故答案為：$\sqrt{2}$．

點評 本題考查拋物線的定義、方程與性質，考查三角形中位線的性質，考查學生的計算能力，屬于中檔題．