
【題目】某工廠的![]() ,
,![]() ,
,![]() 三個不同車間生產同一產品的數量(單位:件)如下表所示.質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測:
三個不同車間生產同一產品的數量(單位:件)如下表所示.質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測:
車間 |
|
|
|
數量 | 50 | 150 | 100 |
(1)求這6件樣品中來自![]() ,
,![]() ,
,![]() 各車間產品的數量;
各車間產品的數量;
(2)若在這6件樣品中隨機抽取2件進行進一步檢測,求這2件產品來自相同車間的概率.
【答案】(1)1,2,3;(2)![]() .
.
【解析】
(1)先求得分層抽樣的抽樣比,由此求得這6件樣品中來自![]() ,
,![]() ,
,![]() 各車間產品的數量.
各車間產品的數量.
(2)利用列舉法,結合古典概型概率計算公式,計算出所求概率.
(1)因為樣本容量與總體中的個體數的比是![]() ,
,
所以![]() 車間產品被選取的件數為
車間產品被選取的件數為![]() ,
,
![]() 車間產品被選取的件數為
車間產品被選取的件數為![]() ,
,
![]() 車間產品被選取的件數為
車間產品被選取的件數為![]() .
.
(2)設6件自![]()
![]()
![]() 三個車間的樣品分別為:
三個車間的樣品分別為:![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() .
.
則從6件樣品中抽取的這2件產品構成的所有基本事件為:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15個.
,共15個.
每個樣品被抽到的機會均等,因此這些基本事件的出現是等可能的.
記事件![]() :“抽取的這2件產品來自相同車間”,
:“抽取的這2件產品來自相同車間”,
則事件![]() 包含的基本事件有:
包含的基本事件有:
![]() ,
,![]() ,
,![]() ,
,![]() ,共4個
,共4個
所以![]() .
.
所以這2件商品來自相同車間的概率為![]() .
.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:
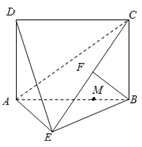
【題目】四邊形ABCD為矩形,AD⊥平面ABE,AE=EB=BC,F為CE上的點,且BF⊥平面ACE.
(1)求證:AE⊥BE;
(2)設M在線段AB上,且滿足AM=2MB,試在線段CE上確定一點N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】魏晉時期數學家劉徽在為《九章算術》作注時,提出利用“牟合方蓋”解決球體體積,“牟合方蓋”由完全相同的四個曲面構成,相對的兩個曲面在同一圓柱的側面上,正視圖和側視圖都是圓,每一個水平截面都是正方形,好似兩個扣合(牟合)在一起的方形傘(方蓋).二百多年后,南北朝時期數學家祖暅在前人研究的基礎上提出了《祖暅原理》:“冪勢既同,則積不容異”.意思是:兩等高立方體,若在每一等高處的截面積都相等,則兩立方體體積相等.如圖有一牟合方蓋,其正視圖與側視圖都是半徑為![]() 的圓,正邊形
的圓,正邊形![]() 是為體現其直觀性所作的輔助線,根據祖暅原理,該牟合方蓋體積為__________.
是為體現其直觀性所作的輔助線,根據祖暅原理,該牟合方蓋體積為__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是半圓
是半圓![]() 的直徑,平面
的直徑,平面![]() 與半圓
與半圓![]() 所在的平面垂直,
所在的平面垂直,![]() ,
,![]() ,
, ![]() ,
,![]() 是半圓
是半圓![]() 上不同于
上不同于![]() ,
,![]() 的點,四邊形
的點,四邊形![]() 是矩形.
是矩形.
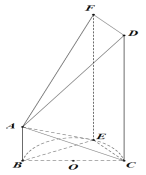
(Ⅰ)若![]() ,證明:
,證明:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求三棱錐
,求三棱錐![]() 體積的最大值.
體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過點![]() ,且與圓
,且與圓![]() 外切于點
外切于點![]() ,過點
,過點![]() 作圓C的兩條切線PM,PN,切點為M,N.
作圓C的兩條切線PM,PN,切點為M,N.
(1)求圓C的標準方程;
(2)試問直線MN是否恒過定點?若過定點,請求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】α,β是兩個不重合的平面,在下列條件中,可判斷平面α,β平行的是( )
A. m,n是平面![]() 內兩條直線,且
內兩條直線,且![]() ,
,![]()
B. ![]() 內不共線的三點到
內不共線的三點到![]() 的距離相等
的距離相等
C. ![]() ,
,![]() 都垂直于平面
都垂直于平面![]()
D. m,n是兩條異面直線,![]() ,
,![]() ,且
,且![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() ,
, ![]() ,
, ![]() .給出以下三個命題:
.給出以下三個命題:
①分別過點![]() ,
, ![]() ,作
,作![]() 的不同于
的不同于![]() 軸的切線,兩切線相交于點
軸的切線,兩切線相交于點![]() ,則點
,則點![]() 的軌跡為橢圓的一部分;
的軌跡為橢圓的一部分;
②若![]() ,
, ![]() 相切于點
相切于點![]() ,則點
,則點![]() 的軌跡恒在定圓上;
的軌跡恒在定圓上;
③若![]() ,
, ![]() 相離,且
相離,且![]() ,則與
,則與![]() ,
, ![]() 都外切的圓的圓心在定橢圓上.
都外切的圓的圓心在定橢圓上.
則以上命題正確的是( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四面體ABCD中,△ABC是等邊三角形,平面ABC⊥平面ABD,點M為棱AB的中點,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求證:AD⊥BC;
(Ⅱ)求異面直線BC與MD所成角的余弦值;
(Ⅲ)求直線CD與平面ABD所成角的正弦值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com