
【題目】四邊形ABCD為矩形,AD⊥平面ABE,AE=EB=BC,F為CE上的點,且BF⊥平面ACE.
(1)求證:AE⊥BE;
(2)設M在線段AB上,且滿足AM=2MB,試在線段CE上確定一點N,使得MN∥平面DAE.
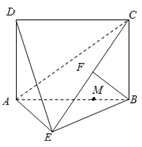
【答案】(1)見解析(2)N點為線段CE上靠近C點的一個三等分點.
【解析】試題分析:(1)由![]() 和
和![]() 平面
平面![]() ,證明
,證明![]() ,再由
,再由![]() 平面
平面![]() 得
得![]() ,根據線面垂直的判定定理證出
,根據線面垂直的判定定理證出![]() 平面
平面![]() ,即證出
,即證出![]() ;(2)在
;(2)在![]() 中過
中過![]() 點作
點作![]() 交
交![]() 于
于![]() 點,在
點,在![]() 中過
中過![]() 點作
點作![]() 交
交![]() 于
于![]() 點,連
點,連![]() ,證明平面
,證明平面![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,從而可得結論.
,從而可得結論.
試題解析:
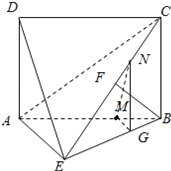
證明:(1)∵BF⊥平面ACE,AE平面ACE,
∴BF⊥AE,BF⊥CE,
∵EB=BC,∴F是CE的中點,
又∵AD⊥平面ABE,AD平面ABCD,
∴平面ABCD⊥平面ABE,
∵平面ABCD∩平面ABE=AB,BC⊥AB
∴BC⊥平面ABE,
從而BC⊥AE,且BC∩BF=B,
∴AE⊥平面BCE,BE平面BCE,
∴AE⊥BE;
(2)在△ABE中過M點作MG∥AE交BE于G點,
在△BEC中過G點作GN∥BC交EC于N點,連MN,
∴CN=![]() CE.
CE.
∵MG∥AE,MG平面ADE,AE平面ADE,
∴MG∥平面ADE.
同理,GN∥平面ADE,且MG與GN交于G點,
∴平面MGN∥平面ADE.
又MN平面MGN,
∴MN∥平面ADE.
故N點為線段CE上靠近C點的一個三等分點.
【方法點晴】本題主要考查線面平行的判定定理、直線和平面垂直的判定定理,屬于難題.證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質,即兩平面平行,在其中一平面內的直線平行于另一平面.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
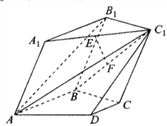
【題目】在如圖所示的多面體中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為邊長為2的菱形,
為邊長為2的菱形, ![]() 為直角梯形,四邊形
為直角梯形,四邊形![]() 為平行四邊形,且
為平行四邊形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數![]() 滿足
滿足![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若函數![]() ,是否存在實數
,是否存在實數![]() 使得
使得![]() 的最小值為0?若存在,求出
的最小值為0?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(3)若函數![]() ,是否存在實數
,是否存在實數![]() ,使函數
,使函數![]() 在
在![]() 上的值域為
上的值域為![]() ?若存在,求出實數
?若存在,求出實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】借助計算器填寫下表:
|
|
|
|
|
0 | ||||
1 | ||||
10 | ||||
20 | ||||
30 | ||||
50 | ||||
70 | ||||
100 | ||||
150 | ||||
200 | ||||
250 | ||||
300 |
觀察表中的變化并歸納各函數遞增的規律:
(1)一次函數![]() 與冪函數
與冪函數![]() 之間比較得出的規律;
之間比較得出的規律;
(2)冪函數![]() 與指數函數
與指數函數![]() 之間比較得出的規律;
之間比較得出的規律;
(3)指數函數![]() 與
與![]() 之間比較得出的規律.
之間比較得出的規律.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地居民用水采用階梯水價,其標準為:每戶每月用水量不超過15噸的部分,每噸3元;超過15噸但不超過25噸的部分,每噸4.5元;超過25噸的部分,每噸6元.
(1)求某戶居民每月需交水費![]() (元)關于用水量
(元)關于用水量![]() (噸)的函數關系式;
(噸)的函數關系式;
(2)若![]() 戶居民某月交水費67.5元,求
戶居民某月交水費67.5元,求![]() 戶居民該月的用水量.
戶居民該月的用水量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的![]() ,
,![]() ,
,![]() 三個不同車間生產同一產品的數量(單位:件)如下表所示.質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測:
三個不同車間生產同一產品的數量(單位:件)如下表所示.質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測:
車間 |
|
|
|
數量 | 50 | 150 | 100 |
(1)求這6件樣品中來自![]() ,
,![]() ,
,![]() 各車間產品的數量;
各車間產品的數量;
(2)若在這6件樣品中隨機抽取2件進行進一步檢測,求這2件產品來自相同車間的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com