
分析 (1)利用二次函數的性質,列出不等式求解即可.
(2)通過韋達定理轉化列出不等式組求解即可.
解答 解:(1)設f(x)=x2+mx+m2-3,方程x2+mx+m2-3=0的實數根分別為x1,x2,且x1<1<x2,可得,f(1)<0,
即:m2+m-2<0,解得-2<m<1,
∴G=(-2,1).
(2)由已知可得x1+x2=-m;x1•x2=m2-3,
∴x12+x22=(x1+x2)2-2x1x2=-m2+6,
由(1)m∈(-2,1),-m2∈(-4,0].-m2+6∈(2,6],
∴x12+x22的取值范圍是(2,6],∵x∈(1,4),
∴x+a∈(1+a,4+a),存在m∈G,x∈{1,4},使得x12+x22=x+a,
∴(2,6]∩(1+a,4+a)≠∅
∴$\left\{\begin{array}{l}{1+a<6}\\{2<4+a}\end{array}\right.$,
∴a的取值范圍是(-2,5).
點評 本題考查零點判定定理以及二次函數的性質的應用,集合的應用,考查轉化思想以及計算能力.


科目:高中數學 來源: 題型:解答題
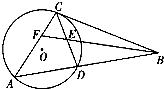 如圖,D是△ABC邊AB上的一點,△ACD內接于圓O,且∠CAD=∠BCD,E是CD的中點,BE的延長線交AC于點F,證明:
如圖,D是△ABC邊AB上的一點,△ACD內接于圓O,且∠CAD=∠BCD,E是CD的中點,BE的延長線交AC于點F,證明:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
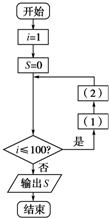 如圖是求從1到100中所有自然數的平方和而設計的程序框圖,將空白處補充完整,并指明它是循環結構中的哪一種類型,且畫出它的另一種結構框圖.
如圖是求從1到100中所有自然數的平方和而設計的程序框圖,將空白處補充完整,并指明它是循環結構中的哪一種類型,且畫出它的另一種結構框圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{7}{2}$ | B. | 2 | C. | -$\frac{13}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=$\left\{\begin{array}{l}-\frac{1}{2}{x^2}-2x({x≤0})\\{(\frac{1}{2})^x}+1({x>0})\end{array}$.
已知函數f(x)=$\left\{\begin{array}{l}-\frac{1}{2}{x^2}-2x({x≤0})\\{(\frac{1}{2})^x}+1({x>0})\end{array}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
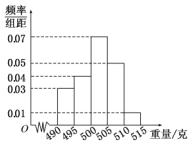 某食品廠為了檢查一條自動包裝流水線的生產情況,隨機抽取該流水線上40件產品作為樣本稱出它們的重量(單位:克),重量的分組區間為 (490,495],(495,500],…,(510,515],由此得到樣本的頻率分布直方圖,如圖所示.
某食品廠為了檢查一條自動包裝流水線的生產情況,隨機抽取該流水線上40件產品作為樣本稱出它們的重量(單位:克),重量的分組區間為 (490,495],(495,500],…,(510,515],由此得到樣本的頻率分布直方圖,如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com