
分析 (1)由不等式可得$\frac{m-1}{2}≤x≤\frac{m+1}{2}$,結合題意應有$\left\{{\begin{array}{l}{2<\frac{m-1}{2}≤3}\\{3≤\frac{m+1}{2}<4}\end{array}}\right.$,由此求得整數m的范圍.
(2)根據題意有${a^4}+{b^4}+{c^4}=\frac{3}{2}$,再利用二維形式的柯西不等式求得a2+b2+c2的最大值.
解答 (1)由關于x的不等式|2x-m|≤1,可得$\frac{m-1}{2}≤x≤\frac{m+1}{2}$,
∵關于x的不等式|2x-m|≤1的整數解有且僅有一個值為3,
則$\left\{{\begin{array}{l}{2<\frac{m-1}{2}≤3}\\{3≤\frac{m+1}{2}<4}\end{array}}\right.$,即5<m<7,又m為整數,則m=6.
(2)由4a4+4b4+4c4=6有${a^4}+{b^4}+{c^4}=\frac{3}{2}$,
由柯西不等式有${({{a^2}+{b^2}+{c^2}})^2}≤({{1^2}+{1^2}+{1^2}})({{{({a^2})}^2}+{{({b^2})}^2}+{{({c^2})}^2}})=\frac{9}{2}$,
當且僅當$a=b=c=\root{4}{{\frac{1}{2}}}$時,等號成立,
所以a2+b2+c2的最大值為$\frac{{3\sqrt{2}}}{2}$.
點評 本題主要考查絕對值不等式的解法,二維形式的柯西不等式的應用,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
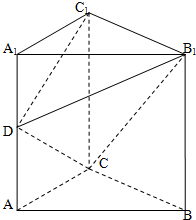 如圖在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D為AA1的中點.
如圖在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D為AA1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ | B. | $\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$ | C. | ${x}^{2}+\frac{{y}^{2}}{2}=1$ | D. | $\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com