
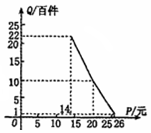
 某消費品專賣店的經營資料顯示如下:
某消費品專賣店的經營資料顯示如下:分析 (1)利用帶待定系數法即可求出函數的解析式,再根據銷售量Q(百件)與銷售價格P(元)滿足的函數關系式,即可月銷量Q(百件)與銷售價格P(元)的函數關系,
(2)設該店月利潤為L元,則由題設得L=Q(P-14)×100-100,得到函數的解析式,分段求出函數的最值,比較即可.
解答 解:(1)∵點(14,22),(20,10),(26,1)在函數的圖象上,
∴$\left\{\begin{array}{l}{14{k}_{1}+{b}_{1}=22}\\{20{k}_{1}+{b}_{1}=10}\end{array}\right.$,解得$\left\{\begin{array}{l}{{k}_{1}=-2}\\{{b}_{1}=50}\end{array}\right.$.
同理可得$\left\{\begin{array}{l}{{k}_{2}=-\frac{3}{2}}\\{{b}_{2}=40}\end{array}\right.$,
∴Q=$\left\{\begin{array}{l}{-2P+50,14≤P≤20}\\{-\frac{3}{2}P+40,20<P≤26}\end{array}\right.$,
(2)設該店月利潤為L元,則由題設得L=Q(P-14)×100-100,
由(1)得L=$\left\{\begin{array}{l}{(-2p+50)(P-14)×100-4400,14≤P≤20}\\{(-\frac{3}{2}P+40)(P-14)×100-4400,20<P≤26}\end{array}\right.$,
=$\left\{\begin{array}{l}{-200{P}^{2}+7800P-74400,14≤P≤20}\\{-150{P}^{2}+6100P-10000,20<P≤26}\end{array}\right.$,
當14≤p≤20時,Lmax=1650元,此時P=$\frac{39}{2}$元,
當20<p≤26時,Lmax=$\frac{4850}{3}$元,此時P=$\frac{61}{3}$元,
故當P=$\frac{39}{2}$時,月利潤最大,為1650元.
點評 本題主要考查與函數的應用問題,根據條件建立函數關系,利用二次函數的圖象和性質是即可得到結論.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數 | B. | 偶函數 | C. | 奇函數或偶函數 | D. | 非奇非偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1,-1 | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 60° | C. | 90° | D. | 不確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com