
分析 (1)由f(x)≥0恒成立,求出c與a,b的關系,利用$\frac{f(-2)}{f(2)-f(0)}$,求出函數的解析式.
(2)分類討論轉化f(x)max-f(x)min≤4a,利用單調性,結合不等式求解即可.
解答 解:(1)由f(x)≥0恒成立,得$\left\{\begin{array}{l}{△≤0}\\{a>0}\end{array}\right.$,即$\left\{\begin{array}{l}{c≥\frac{{b}^{2}}{4a}}\\{a>0}\end{array}\right.$,
記T=$\frac{f(-2)}{f(2)-f(0)}$=$\frac{4a-2b+c}{4a+2b}$≥$\frac{4a-2b+\frac{{b}^{2}}{4a}}{4a+2b}$,
設t=$\frac{b}{a}$>1,則T=$\frac{(t-4)^{2}}{8(t+2)}$,再設u=t+2>3,
則T=$\frac{(u-6)^{2}}{8u}$=$\frac{1}{8}$(u-12+$\frac{36}{u}$)≥0.
當b=c=4a時,$\frac{f(-2)}{f(2)-f(0)}$取最小值,此時f(x)=a(x+2)2.
當a=1時,f(x)=(x+2)2.
(2)對任意的x1,x2∈[-3a,-a]都有|g(x1)-g(x2)|≤2a,
即即當x∈[-3a,-a]時,都有g(x)max-g(x)min≤2a,
∵g(x)=a(x2+4x+3),g(-3a)=9a3-12a2+3a,g(-a)=a3-4a2+3a,
①當-a≤-3時,即a≥3時,g(x)在x∈[-3a,-a]上遞減,
且g(x)max-g(x)min≤g(-3a)-f(-a)=8a3-8a2≤2a,
解得$\frac{1-\sqrt{2}}{2}$≤a≤$\frac{1+\sqrt{2}}{2}$,無解
②當-3a≤-3<-a≤-1,即1≤a<3時,要使g(x)max-g(x)min≤2a,
只要g(-3a)=9a3-12a2+3a≤2a,解得$\frac{2-\sqrt{3}}{2}$≤a≤$\frac{2+\sqrt{3}}{2}$
∴1≤a≤$\frac{2+\sqrt{3}}{2}$,
③當-3<-3a<-1<-a,即$\frac{1}{3}$<a<1時,
要使g(x)max-g(x)min≤2a,
只要g(-a)=a3-4a2+3a≤2a,解得2-$\sqrt{3}$≤a≤2+$\sqrt{3}$
∴$\frac{1}{3}$<a<1時,
④當-3a≥-1,即0<a≤$\frac{1}{3}$時,
∴g(x)在x∈[-3a,-a]上遞增,
且g(x)max-g(x)min=g(-a)-g(-3a)=-8a3+8a2≤2a,解得a∈R,
∴所以0<a≤$\frac{1}{3}$.
綜上,a的取值范圍為(0,$\frac{2+\sqrt{3}}{2}$]
點評 本題考查了函數的性質,分類討論思想,關鍵是分清討論的標準,確定最大值最小值即可,屬于中檔題,


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案科目:高中數學 來源: 題型:選擇題
| A. | 5.2 | B. | 6.6 | C. | 7.1 | D. | 8.3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
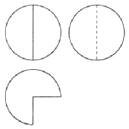 如圖,某幾何體的三視圖由半徑相同的圓和扇形構成,若府視圖中扇形的面積為3π,則該幾何體的體積等于( )
如圖,某幾何體的三視圖由半徑相同的圓和扇形構成,若府視圖中扇形的面積為3π,則該幾何體的體積等于( )| A. | 8π | B. | $\frac{16π}{3}$ | C. | 4π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com