
【題目】設有二元關系![]() ,已知曲線
,已知曲線![]() .
.
(1)若![]() 時,正方形
時,正方形![]() 的四個頂點均在曲線
的四個頂點均在曲線![]() 上,求正方形
上,求正方形![]() 的面積;
的面積;
(2)設曲線![]() 與
與![]() 軸的交點是
軸的交點是![]() ,拋物線
,拋物線![]() 與
與![]() 軸的交點是
軸的交點是![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,求證直線
,求證直線![]() 過定點,并求該定點的坐標;
過定點,并求該定點的坐標;
(3)設曲線![]() 與
與![]() 軸的交點是
軸的交點是![]() ,
,![]() ,可知動點
,可知動點![]() 在某確定的曲線
在某確定的曲線![]() 上運動,曲線
上運動,曲線![]() 上與上述曲線
上與上述曲線![]() 在
在![]() 時共有4個交點,其坐標分別是
時共有4個交點,其坐標分別是![]() 、
、![]() 、
、![]() 、
、![]() ,集合
,集合![]() 的所有非空子集設為
的所有非空子集設為![]() ,將
,將![]() 中的所有元素相加(若
中的所有元素相加(若![]() 只有一個元素,則和是其自身)得到255個數
只有一個元素,則和是其自身)得到255個數![]() ,求所有正整數
,求所有正整數![]() 的值,使得
的值,使得![]() 是一個與變數
是一個與變數![]() 及變數
及變數![]() 均無關的常數.
均無關的常數.
【答案】(1)4;(2)直線![]() 過定點
過定點![]() ;(3)
;(3)![]() 是奇數時,
是奇數時,![]() 是一個與變數
是一個與變數![]() 及變數
及變數![]() 均無關的常數.
均無關的常數.
【解析】
(1)令![]() ,解得
,解得![]() ,即
,即![]() 表示兩條平行直線,這兩條平行線間的距離2為正方形的邊長,由此可得正方形面積;
表示兩條平行直線,這兩條平行線間的距離2為正方形的邊長,由此可得正方形面積;
(2)曲線![]() 中,令
中,令![]() ,則
,則![]() ,設
,設![]() ,由韋達定理得
,由韋達定理得![]() ,寫出
,寫出![]() 的方程求得
的方程求得![]() 的坐標,從而得直線
的坐標,從而得直線![]() 的方程(只含有參數
的方程(只含有參數![]() ),觀察方程可得直線
),觀察方程可得直線![]() 所過定點;
所過定點;
(3)令![]() ,則
,則![]() ,則
,則![]() ,即點
,即點![]() 在曲線
在曲線![]() 上,而曲線
上,而曲線![]() 表示兩條平行線且斜率為1,因此可知點
表示兩條平行線且斜率為1,因此可知點![]() 關于直線
關于直線![]() 對稱,從而可得
對稱,從而可得![]() ,同理
,同理![]() .于是有
.于是有![]() ,有
,有![]() ,則
,則![]() 時,
時,![]() ,對其他244個子集配對:
,對其他244個子集配對:![]() ,滿足
,滿足![]() ,
,![]() ,這樣的集合“對”共有127對。
,這樣的集合“對”共有127對。
以下證明:對![]() 的元素和
的元素和![]() 和
和![]() 的元素和
的元素和![]() ,當
,當![]() 為奇數時,恒有
為奇數時,恒有![]() ,為此可用數學歸納法證明
,為此可用數學歸納法證明![]() 能夠整除
能夠整除![]() ,從而得結論.
,從而得結論.
(1)令![]() ,得
,得![]() ,即
,即![]() 表示兩條平行直線,這兩條平行線間的距離為
表示兩條平行直線,這兩條平行線間的距離為 ,此為正方形的邊長,正方形的面積為4。
,此為正方形的邊長,正方形的面積為4。
(2)在曲線![]() 中,令
中,令![]() ,則
,則![]() ,設
,設![]() ,由韋達定理得
,由韋達定理得![]() ,由題意知
,由題意知![]() ,直線
,直線![]() 方程為
方程為![]() ,
,![]() 方程為
方程為![]() ,
,

由 ,解得
,解得![]() ,同理可得
,同理可得![]() ,∵
,∵![]() ,∴
,∴![]() ,∴直線
,∴直線![]() 方程為
方程為![]() ,化簡為:
,化簡為:![]() ,
,![]() 時,
時,![]() ,故直線
,故直線![]() 過定點
過定點![]() ;
;
(3)令![]() ,則
,則![]() ,則
,則![]() ,即點
,即點![]() 在曲線
在曲線![]() 上,又曲線
上,又曲線![]() :
:![]() 恒表示兩條平行直線
恒表示兩條平行直線![]() ,如圖,
,如圖,
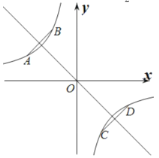
![]() 關于直線
關于直線![]() 對稱,則
對稱,則![]() ,即
,即![]() ,同理
,同理![]() ,則
,則![]() ,集合
,集合![]() 的所有非空子集設為
的所有非空子集設為![]() ,取
,取![]() ,顯然
,顯然![]() ,則
,則![]() 時,
時,![]() ,對
,對![]() 的其他子集,我們把它們配成集合“對”
的其他子集,我們把它們配成集合“對”![]() ,使得
,使得![]() ,
,![]() ,這樣的集合“對”共有127對。
,這樣的集合“對”共有127對。
以下證明:對![]() 的元素和
的元素和![]() 和
和![]() 的元素和
的元素和![]() ,當
,當![]() 為奇數時,恒有
為奇數時,恒有![]() ,為此先證明:
,為此先證明:![]() 是奇數時,則
是奇數時,則![]() 能夠整除
能夠整除![]() ,
,
用數學歸納法證之:
(i)當![]() 時顯然成立,
時顯然成立,
(ii)假設![]() (
(![]() 是奇數)成立,即
是奇數)成立,即![]() 能夠整除
能夠整除![]() ,則當
,則當![]() 時,
時,![]() ,
,
由歸納假設知此式能被![]() 整除,
整除,
由(i)(ii)可知當![]() 為奇數時,
為奇數時,![]() 能夠整除
能夠整除![]() .
.
∴![]() 為奇數時,
為奇數時,![]() (其中
(其中![]() 是關于
是關于![]() 的整式),
的整式),
∵![]() ,
,![]() ,∴對每一個集合“對”
,∴對每一個集合“對”![]() ,
,![]() ,
,
則一定有![]() =0,
=0,![]() ,于是
,于是![]() 是常數.
是常數.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線Γ的準線方程為![]() .焦點為
.焦點為![]() .
.
(1)求證:拋物線Γ上任意一點![]() 的坐標
的坐標![]() 都滿足方程:
都滿足方程:![]()
(2)請求出拋物線Γ的對稱性和范圍,并運用以上方程證明你的結論;
(3)設垂直于![]() 軸的直線與拋物線交于
軸的直線與拋物線交于![]() 兩點,求線段
兩點,求線段![]() 的中點
的中點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在我們的教材必修一中有這樣一個問題,假設你有一筆資金,現有三種投資方案供你選擇,這三種方案的回報如下:
方案一:每天回報![]() 元;
元;
方案二:第一天回報![]() 元,以后每天比前一天多回報
元,以后每天比前一天多回報![]() 元;
元;
方案三:第一天回報![]() 元,以后每天的回報比前一天翻一番.
元,以后每天的回報比前一天翻一番.
記三種方案第![]() 天的回報分別為
天的回報分別為![]() ,
,![]() ,
,![]() .
.
(1)根據數列的定義判斷數列![]() ,
,![]() ,
,![]() 的類型,并據此寫出三個數列的通項公式;
的類型,并據此寫出三個數列的通項公式;
(2)小王準備做一個為期十天的短期投資,他應該選擇哪一種投資方案?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,點
,點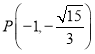 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)是否存在斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,使得
兩點,使得![]() ?若存在,求出直線的方程;若不存在,說明理由.
?若存在,求出直線的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(ax+b)﹣x(a,b∈R,ab≠0).
(1)討論f(x)的單調性;
(2)若f(x)≤0恒成立,求ea(b﹣1)的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com