
分析 (1)通過利用當n≥2時${S_n}={S_{n-1}}+{a_n}={S_{n-1}}+2\sqrt{S_n}-1$可知${S_{n-1}}={(\sqrt{S_n}-1)^2}$,進而可知$\sqrt{S_n}-\sqrt{{S_{n-1}}}=1$,從而${S_n}={n^2}$,an=2n-1;
(2)通過(1)裂項可知$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$,進而并項相加、參數分離可將問題轉化為λ≥$\frac{n}{2({n}^{2}+4n+4)}$=$\frac{1}{2}$•$\frac{1}{n+\frac{4}{n}+4}$對一切n∈N*恒成立,利用基本不等式可得結論.
解答 解:(1)∵正數列{an}的前n項和為Sn,且${a_n}=2\sqrt{S_n}-1$,
∴當n≥2時${S_n}={S_{n-1}}+{a_n}={S_{n-1}}+2\sqrt{S_n}-1$,即${S_{n-1}}={(\sqrt{S_n}-1)^2}$,
因為Sn-1>0,所以$\sqrt{S_n}-\sqrt{{S_{n-1}}}=1$,
又因為$2\sqrt{a_1}={a_1}+1$,解得a1=1,
所以$\sqrt{S_n}=1+(n-1)×1=n$,即${S_n}={n^2}$,
所以an=2n-1;
(2)由(1)可知${b_n}=\frac{{{a_n}+3}}{2}=n+1$,
所以$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$,
所以${T_n}=(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{n+1}-\frac{1}{n+2})=\frac{1}{2}-\frac{1}{n+2}=\frac{n}{2n+4}$,
因為Tn≤λbn+1對一切n∈N*恒成立,
所以$\frac{n}{2n+4}$≤λ(n+2),所以λ≥$\frac{n}{2({n}^{2}+4n+4)}$=$\frac{1}{2}$•$\frac{1}{n+\frac{4}{n}+4}$,
因為$n+\frac{4}{n}$≥2$\sqrt{n•\frac{4}{n}}$=4,當且僅當n=2時取等號,所以λ≥$\frac{1}{16}$,
故實數λ的最小值為$\frac{1}{16}$.
點評 本題考查數列的通項及前n項和,考查階差法,考查裂項相消法,考查基本不等式,對表達式的靈活變形是解決本題的關鍵,注意解題方法的積累,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 2019 | C. | -2019 | D. | 2018×2019 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
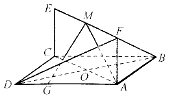 如圖,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G為線段AD上的任意一點.
如圖,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G為線段AD上的任意一點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | n=4時該命題不成立 | |
| B. | n=6時該命題不成立 | |
| C. | n為大于5的某個自然數時該命題成立 | |
| D. | 以上答案均不對 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com