
報廢年限 車型 | 1年 | 2年 | 3年 | 4年 | 總計 |
| A | 20 | 35 | 35 | 10 | 100 |
| B | 10 | 30 | 40 | 20 | 100 |
分析 (Ⅰ)求出回歸系數,可得回歸方程,即可得出結論;
(Ⅱ)分別計算相應的數學期望,即可得出結論.
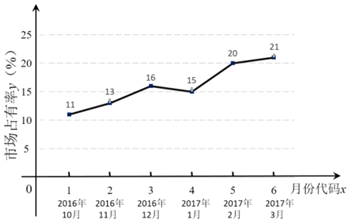
解答 解:(Ⅰ)由題意,$\overline{x}$=3.5,$\overline{y}$=16,$\widehat{b}$=$\frac{35}{17.5}$=2,$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$=16-2×3.5=9,
∴$\widehat{y}$=2x+9,
x=7時,$\widehat{y}$=2×7+9=23,即預測M公司2017年4月份(即x=7時)的市場占有率為23%;
(Ⅱ)由頻率估計概率,每輛A款車可使用1年,2年,3年、4年的概率分別為0.2,0.35,0.35,0.1,
∴每輛A款車的利潤數學期望為(500-1000)×0.2+(1000-1000)×0.35+(1500-1000)×0.35+(2000-1000)×0.1=175元;
每輛B款車可使用1年,2年,3年、4年的概率分別為0.1,0.3,0.4,0.2,
∴每輛B款車的利潤數學期望為(500-1200)×0.1+(1000-1200)×0.3+(1500-1200)×0.4+(2000-1200)×0.2=150元;
∵175>150,
∴應該采購A款車.
點評 本題考查數學知識在實際生活中的應用,考查學生的閱讀能力,對數據的處理能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
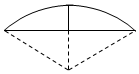 《九章算術》是我國古代數學成就的杰出代表作,其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積=$\frac{1}{2}×$(弦×矢+矢2),弧田(如圖)由圓弧和其所對弦圍城,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角$\frac{2π}{3}$,半徑為6米的弧田,按照上述經驗公式計算所得弧田面積約是($\sqrt{3}≈1.73$)( )
《九章算術》是我國古代數學成就的杰出代表作,其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積=$\frac{1}{2}×$(弦×矢+矢2),弧田(如圖)由圓弧和其所對弦圍城,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角$\frac{2π}{3}$,半徑為6米的弧田,按照上述經驗公式計算所得弧田面積約是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 為了解某地高中生的身高情況,研究小組在該地高中生中隨機抽出30名高中生的身高統計成如圖所示的莖葉圖(單位:cm).
為了解某地高中生的身高情況,研究小組在該地高中生中隨機抽出30名高中生的身高統計成如圖所示的莖葉圖(單位:cm).查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com