Question

5．某研究所計劃利用“神十”宇宙飛船進行新產品搭載實驗，計劃搭載若干件新產品A、B，該所要根據該產品的研制成本、產品重量、搭載實驗費用和預計產生的收益來決定具體搭載安排，有關數據如下表：

	每件產品A	每件產品B
研制成本、搭載 費用之和（萬元）	20	30	計劃最大資金額 300萬元
產品重量（千克）	10	5	最大搭載重量110千克
預計收益（萬元）	80	60

分別用x，y表示搭載新產品A，B的件數．總收益用Z表示
（Ⅰ）用x，y列出滿足生產條件的數學關系式，并畫出相應的平面區域；
（Ⅱ）問分別搭載新產品A、B各多少件，才能使總預計收益達到最大？并求出此最大收益．

Answer 1

分析 （Ⅰ）由題意，列出關于x，y的不等式組，由不等式組得到平面區域即可；
（Ⅱ）列出目標函數，根據（Ⅰ）的約束條件以及可行域，結合目標函數的幾何意義求最大值即可．

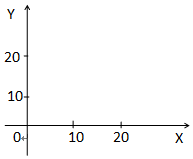
解答 解：（Ⅰ）解：由已知x，y滿足的數學關系式為$\left\{{\begin{array}{l}{20x+30y≤300}\\{10x+5y≤110}\\{x≥0}\\{y≥0}\end{array}}\right.$，且x∈N，y∈N，
該二元一次不等式組所表示的區域為圖中的陰影部分．…（6分）

（Ⅱ）解：設最大收益為z萬元，則目標函數z=80x+60y．
作出直線l_a：4x+3y=0并平移，由圖象知，
當直線經過M點時，z能取到最大值，
由$\left\{{\begin{array}{l}{2x+3y=30}\\{2x+y=22}\end{array}}\right.$解得$\left\{{\begin{array}{l}{x=9}\\{y=4}\end{array}}\right.$且滿足x∈N，y∈N，即M（9，4）是最優解，
所以z_max=80×9+60×4=960（萬元），
答：搭載A產品9件，B產品4件，能使總預計收益達到最大值，最大預計收益為960萬元．…（12分）

點評 本題考查了簡單線性規劃問題的解決收益最大；關鍵是正確列出約束條件以及目標函數，利用數形結合的方法求最值．