
 已知函數f(x)=cos(2x-$\frac{π}{3}$)+2sin(x-$\frac{π}{4}$)sin(x+$\frac{π}{4}$).
已知函數f(x)=cos(2x-$\frac{π}{3}$)+2sin(x-$\frac{π}{4}$)sin(x+$\frac{π}{4}$).分析 (1)將函數化為y=Asin(ωx+φ)的形式,再利用周期公式求函數的最小正周期,最后將內層函數看作整體,放到正弦函數的增區間上,解不等式得函數的單調遞增區間;
(2)“五點畫法”列表,描點,連線.
解答 解:函數f(x)=cos(2x-$\frac{π}{3}$)+2sin(x-$\frac{π}{4}$)sin(x+$\frac{π}{4}$).
化簡得:$f(x)=cos(2x-\frac{π}{3})+2sin(x-\frac{π}{4})sin(x+\frac{π}{4})=sin(2x-\frac{π}{6})$,
函數的最小正周期T=$\frac{2π}{ω}=\frac{2π}{2}$=π,
由正弦函數圖象及性質可知:$2x-\frac{π}{6}$∈[$2kπ-\frac{π}{2}$,$2kπ+\frac{π}{2}$](k∈Z)是單調增區間,
即$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}⇒kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}$,
故函數f(x)的增區間為:$[{kπ-\frac{π}{6},kπ+\frac{π}{3}}](k∈Z)$.
(2)列表得:
| x | $-\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| $2x-\frac{π}{6}$ | $-\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ |
| y | -1 | 0 | 1 | 0 | -1 |
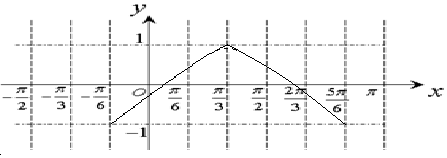
點評 本題主要考查利用y=Asin(ωx+φ)的圖象特征,由函數y=Asin(ωx+φ)的部分圖象求解析式,會利用五點畫法描圖,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
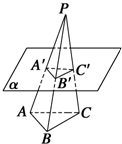 如圖所示,P是三角形ABC所在平面外一點,平面α∥平面ABC,α分別交線段PA、PB、PC于A′、B′、C′,若PA′:AA′=3:4,則S△A′B′C′:S△ABC=9:49.
如圖所示,P是三角形ABC所在平面外一點,平面α∥平面ABC,α分別交線段PA、PB、PC于A′、B′、C′,若PA′:AA′=3:4,則S△A′B′C′:S△ABC=9:49.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
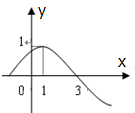 函數f(x)=sin(ωx+φ),(x∈R,ω>0,0<φ<π)的部分圖象如圖所示,則( )
函數f(x)=sin(ωx+φ),(x∈R,ω>0,0<φ<π)的部分圖象如圖所示,則( )| A. | $ω=\frac{π}{2},φ=\frac{π}{4}$ | B. | $ω=\frac{π}{3},φ=\frac{π}{6}$ | C. | $ω=\frac{π}{4},φ=\frac{π}{4}$ | D. | $ω=\frac{π}{4},φ=\frac{3π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1008 | B. | 1010 | C. | $\frac{2019}{2}$ | D. | 2019 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某研究所計劃利用“神十”宇宙飛船進行新產品搭載實驗,計劃搭載若干件新產品A、B,該所要根據該產品的研制成本、產品重量、搭載實驗費用和預計產生的收益來決定具體搭載安排,有關數據如下表:
某研究所計劃利用“神十”宇宙飛船進行新產品搭載實驗,計劃搭載若干件新產品A、B,該所要根據該產品的研制成本、產品重量、搭載實驗費用和預計產生的收益來決定具體搭載安排,有關數據如下表:| 每件產品A | 每件產品B | ||
| 研制成本、搭載 費用之和(萬元) | 20 | 30 | 計劃最大資金額 300萬元 |
| 產品重量(千克) | 10 | 5 | 最大搭載重量110千克 |
| 預計收益(萬元) | 80 | 60 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com