
| A. | -1 | B. | 1 | C. | -i | D. | i |
分析 由復數代數形式的乘除運算化簡復數$z=\frac{m+i}{1+i}$,結合已知條件求出m的值,然后代入復數$z=\frac{m+i}{1+i}$化簡即可求出z,則復數z的共軛復數的虛部可求.
解答 解:∵$z=\frac{m+i}{1+i}$=$\frac{(m+i)(1-i)}{(1+i)(1-i)}=\frac{1+m+(1-m)i}{2}$=$\frac{1+m}{2}+\frac{1-m}{2}i$是純虛數,
∴$\left\{\begin{array}{l}{\frac{1+m}{2}=0}\\{\frac{1-m}{2}≠0}\end{array}\right.$,解得m=-1.
∴$z=\frac{-1+i}{1+i}=\frac{(-1+i)(1-i)}{(1+i)(1-i)}=\frac{2i}{2}=i$.
則$\overline{z}=-i$.
∴復數z的共軛復數的虛部是-1.
故選:A.
點評 本題考查了復數代數形式的乘除運算,考查了復數的基本概念,是基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\overrightarrow{CB}$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{BC}$ | D. | $\overrightarrow O$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 6 | D. | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
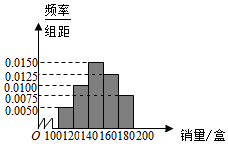 某大學在開學季準備銷售一種盒飯進行試創業,在一個開學季內,每售出1盒該盒飯獲利潤10元,未售出的產品,每盒虧損5元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了150盒該產品,以x(單位:盒,100≤x≤200)表示這個開學季內的市場需求量,y(單位:元)表示這個開學季內經銷該產品的利潤.
某大學在開學季準備銷售一種盒飯進行試創業,在一個開學季內,每售出1盒該盒飯獲利潤10元,未售出的產品,每盒虧損5元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了150盒該產品,以x(單位:盒,100≤x≤200)表示這個開學季內的市場需求量,y(單位:元)表示這個開學季內經銷該產品的利潤.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com