
分析 (1)根據(jù)向量的夾角公式即可求出角B的大小;
(2)利用正弦定理把邊變化為角,利用三角函數(shù)的有界限即可求解取值范圍
解答 解:(1)向量$\overrightarrow m$=(sinB,cosB)與向量$\overrightarrow n=(0,\;-1)$的夾角為$\frac{π}{3}$,
∴$\overrightarrow{m}•\overrightarrow{n}=\left|\overrightarrow{m}\right|•\left|\overrightarrow{n}\right|•cos\frac{π}{3}$,
即:-cosB=$\frac{1}{2}$,
∴cosB=-$\frac{1}{2}$
∵0<B<π,
∴B=$\frac{2π}{3}$.
(2)由正弦定理,可得:$\frac{a+c}{b}$=$\frac{sinA+sinC}{sinB}$
=$\frac{2}{\sqrt{3}}$[sinA+sin($\frac{π}{3}$-A)]=$\frac{2}{\sqrt{3}}$(sinA+$\frac{\sqrt{3}}{2}$cosA-$\frac{1}{2}$sinA)
=$\frac{2}{\sqrt{3}}$sin(A+$\frac{π}{3}$)
∵0<A<$\frac{π}{3}$,
∴$\frac{π}{3}$<A+$\frac{π}{3}$<$\frac{2π}{3}$,
∴$\frac{\sqrt{3}}{2}$<sin(A+$\frac{π}{3}$)≤1,
∴1<$\frac{a+c}{b}$≤$\frac{2\sqrt{3}}{3}$,
故$\frac{a+c}{b}$的取值范圍為(1,$\frac{2\sqrt{3}}{3}$].
點評 本題考查向量的夾角公式,三角形的正弦定理的運用,三角函數(shù)的有界性,考查運算能力,屬于基礎(chǔ)題.


科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | -$\frac{8}{15}$ | B. | -$\frac{29}{15}$ | C. | -$\frac{27}{20}$ | D. | $\frac{1}{20}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
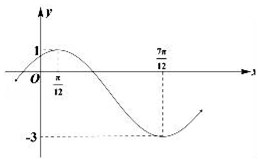 已知函數(shù)f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示:
已知函數(shù)f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示:查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com