
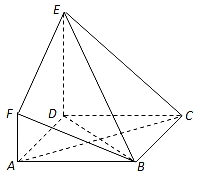
 如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.
如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.分析 (Ⅰ)推導出AC⊥BD,AC⊥DE,由此能證明AC⊥平面BDE.
(Ⅱ)該幾何體的體積V=VB-AEF+VE-ABCD,由此能求出該幾何體的體積.
解答 證明:(Ⅰ)∵ABCD是邊長為3的正方形,∴AC⊥BD,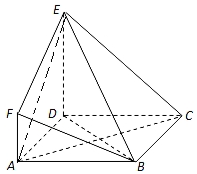
∵DE⊥平面ABCD,AC?平面ABCD,
∴AC⊥DE,
∵BD∩DE=D,∴AC⊥平面BDE.
解:(Ⅱ)∵ABCD是邊長為3的正方形,AF∥DE,DE=3AF,
BE與平面ABCD所成角為60°.
∴BD=$\sqrt{9+9}$=3$\sqrt{2}$,ED=3$\sqrt{6}$,AF=$\sqrt{6}$,
由題意得DE⊥平面ABCD,AB⊥平面AEF,
∴該幾何體的體積:
V=VB-AEF+VE-ABCD
=$\frac{1}{3}×3×[\frac{1}{2}(\sqrt{6}+3\sqrt{6})×3-\frac{1}{2}×3×3\sqrt{6}]$+$\frac{1}{3}×3\sqrt{6}×{3}^{2}$
=$\frac{21\sqrt{6}}{2}$.
點評 本題考查線面垂直的證明,考查幾何體的體積的求法,涉及到空間中線線、線面、面面間的位置關系等基礎知識,考查推理論證能力、運算求解能力、空間想象能力,考查化歸與轉化思想,是中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
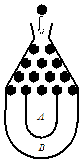 將一個半徑適當的小球放入如圖所示的容器最上方的入口處,小球將自由下落.小球在下落過程中它將3次遇到黑色障礙物,最后落入A袋或B袋中.已知小球每次遇到黑色障礙物時,向左、右兩邊下落的概率都是$\frac{1}{2}$.
將一個半徑適當的小球放入如圖所示的容器最上方的入口處,小球將自由下落.小球在下落過程中它將3次遇到黑色障礙物,最后落入A袋或B袋中.已知小球每次遇到黑色障礙物時,向左、右兩邊下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某特色餐館開通了美團外賣服務,在一周內的某特色外賣份數x(份)與收入y(元)之間有如下的對應數據:
某特色餐館開通了美團外賣服務,在一周內的某特色外賣份數x(份)與收入y(元)之間有如下的對應數據:| 外賣份數x(份) | 2 | 4 | 5 | 6 | 8 |
| 收入y(元) | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
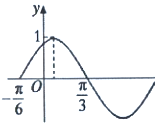 函數$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分圖象如圖所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),則f(x1+x2)=( )
函數$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分圖象如圖所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),則f(x1+x2)=( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com