
分析 (1)化簡函數為分段函數,利用函數的單調性求解函數的最小值,然后求解m即可.
(2)利用$\frac{1}{a}+\frac{1}{b}=2$,轉化推出ab的范圍,化簡$(a+1)(b+1)=\frac{7}{2}$,推出ab的范圍,即可得到結果.
解答 解:(1)因為$f(x)=|{x+1}|+x-m=\left\{\begin{array}{l}2x+1-m,x≥-1\\-1-m,x<-1\end{array}\right.$,x≥-1時,函數是增函數,
所以ymin=-1-m=-3⇒m=2.
(2)∵$\frac{1}{a}+\frac{1}{b}=2$,∴$a+b=2ab≥2\sqrt{ab}⇒ab≥1$,
∵$(a+1)(b+1)=a+b+ab+1=3ab+1=\frac{7}{2}$,
∴$ab=\frac{5}{6}<1$,矛盾.
所以不存在正實數a,b滿足條件.
點評 本題考查分段函數的應用,函數的最值以及基本不等式的應用,考查計算能力.


 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 3 | C. | -$\frac{9}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 月利潤(單位:千萬元) | -0.2 | -0.1 | 0 | 0.1 | 0.3 |
| 頻數 | 2 | 1 | 2 | 4 | 1 |
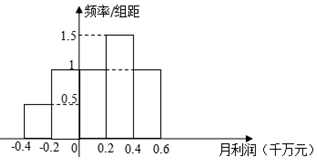
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,2] | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{6}$,2] | D. | [$\frac{1}{9}$,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
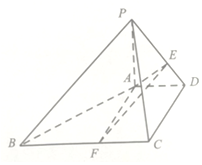 如圖,在四棱錐P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是線段PD上的點,設PE=λPD,F是BC上的點,且AF∥CD
如圖,在四棱錐P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是線段PD上的點,設PE=λPD,F是BC上的點,且AF∥CD查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|2≤x≤3} | B. | {x|x≤2或x≥3} | C. | {x|2<x≤3} | D. | {x|x<2或x≥3} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com