
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
分析 求定積分得a的值,再利用二項式展開式的通項公式求出展開式的常數項.
解答 解:$a=\int_0^2{xdx}$=$\frac{1}{2}$x2${|}_{0}^{2}$=$\frac{1}{2}$×22=2,
∴二項式${(x-\frac{a+1}{x})^6}$=${(x-\frac{3}{x})}^{6}$展開式中,
通項公式為Tr+1=${C}_{6}^{r}$•x6-r•${(-\frac{3}{x})}^{r}$=(-3)r•${C}_{6}^{r}$•x6-2r,
令6-2r=0,解得r=3;
∴展開式的常數項為:
T4=(-3)3•${C}_{6}^{3}$=-540.
故選:C.
點評 本題考查了定積分的計算問題,也考查了二項式展開式的通項公式應用問題,是基礎題.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源: 題型:解答題
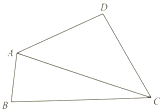 在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({\sqrt{6},\sqrt{7}}]$ | B. | $({0,\sqrt{7}}]$ | C. | $({\frac{{2\sqrt{42}}}{5},\sqrt{7}}]$ | D. | (6,7] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com