
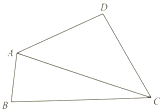
 在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.分析 (1)△ACD中,由余弦定理可得:AC2=${2}^{2}×2-2×{2}^{2}×(-\frac{1}{7})$=$\frac{64}{7}$,解得AC.可得cos∠DAC=$\frac{\frac{1}{2}AC}{AD}$.
(2)設∠DAC=α=∠DCA.由(1)可得:cosα=$\frac{2\sqrt{7}}{7}$,sinα=$\frac{\sqrt{21}}{7}$.可得sin∠BAC=sin(120°-α).sinB=sin(∠BAC+∠BCA)=sin(180°-2α)=sin2α.在△BAC中,由正弦定理可得:$\frac{BC}{sin∠BAC}$=$\frac{AC}{sinB}$.即可得出.
解答 解:(1)△ACD中,由余弦定理可得:AC2=${2}^{2}×2-2×{2}^{2}×(-\frac{1}{7})$=$\frac{64}{7}$,解得AC=$\frac{8\sqrt{7}}{7}$.
∴cos∠DAC=$\frac{\frac{1}{2}AC}{AD}$=$\frac{\frac{1}{2}×\frac{8\sqrt{7}}{7}}{2}$=$\frac{2\sqrt{7}}{7}$.
(2)設∠DAC=α=∠DCA.
由(1)可得:cosα=$\frac{2\sqrt{7}}{7}$,sinα=$\frac{\sqrt{21}}{7}$.
∴sin∠BAC=sin(120°-α)=$\frac{\sqrt{3}}{2}$×$\frac{2\sqrt{7}}{7}$+$\frac{1}{2}×\frac{\sqrt{21}}{7}$=$\frac{3\sqrt{21}}{14}$.
∴sinB=sin(∠BAC+∠BCA)=sin(180°-2α)=sin2α=2×$\frac{2\sqrt{7}}{7}$×$\frac{\sqrt{21}}{7}$=$\frac{4\sqrt{3}}{7}$.
在△BAC中,由正弦定理可得:$\frac{BC}{sin∠BAC}$=$\frac{AC}{sinB}$.
∴BC=$\frac{\frac{8\sqrt{7}}{7}×\frac{3\sqrt{21}}{14}}{\frac{4\sqrt{3}}{7}}$=3.
點評 本題考查了正弦定理余弦定理、和差公式、三角形內角和定理、誘導公式、等腰三角形的性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 有極大值,無極小值 | B. | 有極小值,無極大值 | ||
| C. | 既有極大值又有極小值 | D. | 既無極大值也無極小值 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 100 | B. | 900 | C. | 999 | D. | 1000 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{1}{2}$,3) | B. | (-∞,$\frac{1}{2}$]∪(3,+∞) | C. | [$\frac{1}{3}$,2] | D. | (-∞,$\frac{1}{3}$]∪[2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,2) | B. | (1,+∞) | C. | (0,1) | D. | (-∞,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 3 | C. | -$\frac{9}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 總體是指這箱1000袋方便面 | B. | 個體是一袋方便面 | ||
| C. | 樣本是按2%抽取的20袋方便面 | D. | 樣本容量為20 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
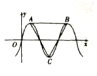 函數$f(x)=3\sqrt{3}sinωx({ω>0})$的部分圖象如圖所示,點A,B是圖象的最高點,點C是圖象的最低點,且△ABC是正三角形,則f(1)+f(2)+f(3)的值為( )
函數$f(x)=3\sqrt{3}sinωx({ω>0})$的部分圖象如圖所示,點A,B是圖象的最高點,點C是圖象的最低點,且△ABC是正三角形,則f(1)+f(2)+f(3)的值為( )| A. | $\frac{9}{2}$ | B. | $\frac{{9\sqrt{3}}}{2}$ | C. | $9\sqrt{3}+1$ | D. | $\frac{{9({\sqrt{3}+1})}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com