
| A. | (0,2) | B. | (1,+∞) | C. | (0,1) | D. | (-∞,2) |
分析 作出區域D,曲線y=ax2+1表示過點A(0,1)的拋物線,可行域存在無數個點滿足拋物線,列出關系式求解可得.
解答 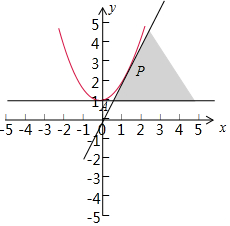 解:作出約束條件不等式$\left\{\begin{array}{l}{y>1}\\{2x-y≥0}\end{array}\right.$所對應的可行域D(如圖陰影),
解:作出約束條件不等式$\left\{\begin{array}{l}{y>1}\\{2x-y≥0}\end{array}\right.$所對應的可行域D(如圖陰影),
曲線y=ax2+1上存在無數個點在D內,可知直線2x-y=0與拋物線相切是臨界點,如圖紅色曲線下方滿足題意,
設切點為P(m,2m),
y′=2ax,可得2am=2,2m=am2+1,可得m=1,
解得a=1,
可解得A(1,1),
結合圖象可得要使y=ax2+1與D內存在無數個點落在D上,可得0<a<1,
故選:C.
點評 本題考查簡單線性規劃,數形結合是解決問題的關鍵,屬中檔題.


科目:高中數學 來源: 題型:填空題
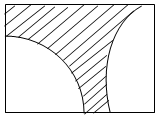 已知矩形的長為10,寬為5(如圖所示),在矩形內隨機地投擲1000顆黃豆,數得落在陰影部分的黃豆為560顆,則可以估計陰影部分的面積為2.8.
已知矩形的長為10,寬為5(如圖所示),在矩形內隨機地投擲1000顆黃豆,數得落在陰影部分的黃豆為560顆,則可以估計陰影部分的面積為2.8.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
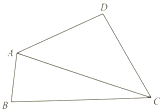 在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四邊形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | $\sqrt{2}$+$\frac{1}{2}$ | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | m(1+q)4元 | B. | m(1+q)5元 | C. | $\frac{m[(1+q)^{4}-(1+q)]}{q}$元 | D. | $\frac{m[(1+q)^{5}-(1+q)]}{q}$元 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com