
分析 (1)根據橢圓的定義和性質,建立方程求出a,b即可.
(2)聯立直線和橢圓方程,利用消元法結合設而不求的思想進行求解即可.
解答 解:(Ⅰ)∵點Q 在線段AP 的垂直平分線上,∴|AQ|=|PQ|.
又|CP|=|CQ|+|QP|=2$\sqrt{2}$,∴|CQ|+|QA|=2$\sqrt{2}$>|CA|=2.
∴曲線E是以坐標原點為中心,C(-1,0)和A(1,0)為焦點,長軸長為2$\sqrt{2}$ 的橢圓.
設曲線E 的方程為$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).
∵c=1,a=$\sqrt{2}$,∴b2=2-1=1.
∴曲線 E的方程為$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(Ⅱ)設M(x1,y1),N(x2,y2).
聯立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$ 消去y,得(1+2k2)x2+4kmx+2m2-2=0.
此時有△=16k2-8m2+8>0.
由一元二次方程根與系數的關系,得x1+x2=$\frac{-4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,.
∴|MN|=$\sqrt{1+{k}^{2}}•\sqrt{(\frac{-4km}{1+2{k}^{2}})^{2}-4×\frac{2{m}^{2}-2}{1+2{k}^{2}}}$=$\frac{\sqrt{1+{k}^{2}}}{1+2{k}^{2}}$$•\sqrt{8(2{k}^{2}-{m}^{2}+1)}$
∵原點O到直線l的距離d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$-,
∴S△MON=$\frac{1}{2}|MN|•d$=$\frac{\sqrt{2}}{1+2{k}^{2}}$.$\sqrt{{m}^{2}(2{k}^{2}-{m}^{2}+1)}$,由△>0,得2k2-m2+1>0.
又m≠0,
∴據基本不等式,得S△MON=$\frac{\sqrt{2}}{1+2{k}^{2}}$.$\sqrt{{m}^{2}(2{k}^{2}-{m}^{2}+1)}$≤$\frac{\sqrt{2}}{1+2{k}^{2}}$$•\frac{{m}^{2}+2{k}^{2}-{m}^{2}+1}{2}$=$\frac{\sqrt{2}}{2}$,
當且僅當m2=$\frac{2{k}^{2}+1}{2}$時,不等式取等號.
∴△MON面積的最大值為$\frac{\sqrt{2}}{2}$.
點評 本題主要考查與橢圓有關的軌跡方程問題,以及直線和橢圓的位置關系的應用,利用消元法以及設而不求的數學思想是解決本題的關鍵.,運算量較大,有一定的難度.


科目:高中數學 來源: 題型:選擇題
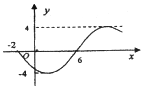
| A. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | B. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | C. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | -2 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
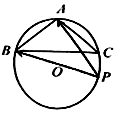 如圖,在△A BC中,三內角 A,B,C的對邊分別為a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S為△A BC的面積,圓 O是△A BC的外接圓,P是圓 O上一動點,
如圖,在△A BC中,三內角 A,B,C的對邊分別為a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S為△A BC的面積,圓 O是△A BC的外接圓,P是圓 O上一動點,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com