
 如圖,已知等邊△ABC的邊長為2,⊙A的半徑為1,PQ為⊙A的任一條直徑,則$\overrightarrow{BP}$•$\overrightarrow{CQ}$-$\overrightarrow{AP}$•$\overrightarrow{CB}$的值為( )
如圖,已知等邊△ABC的邊長為2,⊙A的半徑為1,PQ為⊙A的任一條直徑,則$\overrightarrow{BP}$•$\overrightarrow{CQ}$-$\overrightarrow{AP}$•$\overrightarrow{CB}$的值為( )| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
分析 由題意可得$\overrightarrow{AQ}$=-$\overrightarrow{AP}$,|$\overrightarrow{AP}$|=1,$\overrightarrow{AB}•\overrightarrow{AC}$=2,再根據 $\overrightarrow{BP}$•$\overrightarrow{CQ}$-$\overrightarrow{AP}$•$\overrightarrow{CB}$=($\overrightarrow{AP}-\overrightarrow{AB}$)•($\overrightarrow{AQ}-\overrightarrow{AC}$)-$\overrightarrow{AP}$•(-$\overrightarrow{AC}$+$\overrightarrow{AB}$),計算求得結果.
解答 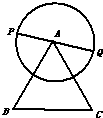 解:等邊△ABC的邊長為2,⊙A的半徑為1,PQ為⊙A的任一條直徑,如圖所示:
解:等邊△ABC的邊長為2,⊙A的半徑為1,PQ為⊙A的任一條直徑,如圖所示:
∴$\overrightarrow{AQ}$=-$\overrightarrow{AP}$,|$\overrightarrow{AP}$|=1,$\overrightarrow{AB}•\overrightarrow{AC}$=2•2•cos60°=2,
∴$\overrightarrow{BP}$•$\overrightarrow{CQ}$-$\overrightarrow{AP}$•$\overrightarrow{CB}$=($\overrightarrow{AP}-\overrightarrow{AB}$)•($\overrightarrow{AQ}-\overrightarrow{AC}$)-$\overrightarrow{AP}$•(-$\overrightarrow{AC}$+$\overrightarrow{AB}$)=$\overline{AP}•\overrightarrow{AQ}$-$\overrightarrow{AP}•\overrightarrow{AC}$-$\overrightarrow{AB}•\overrightarrow{AQ}$+$\overrightarrow{AB}•\overrightarrow{AC}$+$\overrightarrow{AP}•\overrightarrow{AC}$-$\overrightarrow{AP}•\overrightarrow{AB}$
=$\overline{AP}•\overrightarrow{AQ}$-$\overrightarrow{AB}•\overrightarrow{AQ}$+$\overrightarrow{AB}•\overrightarrow{AC}$-$\overrightarrow{AP}•\overrightarrow{AB}$=-${\overrightarrow{AP}}^{2}$+$\overrightarrow{AP}•\overrightarrow{AB}$+$\overrightarrow{AB}•\overrightarrow{AC}$-$\overrightarrow{AP}•\overrightarrow{AB}$=-${\overrightarrow{AP}}^{2}$+$\overrightarrow{AB}•\overrightarrow{AC}$=-1+2=1,
故選:B.
點評 本題主要考查向量知識在幾何中的應用問題.一般在求解此類問題時,常用三角形法則或平行四邊形法則把問題轉化,屬于中檔題.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 3 或-4 | C. | -1 | D. | 6 或10 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10000001110(2) | B. | 10000011110(2) | C. | 100000011101(2) | D. | 10000001100(2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
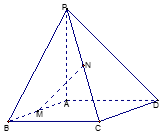 已知PA垂直于矩形ABCD所在平面,M,N分別是AB,PC的中點.
已知PA垂直于矩形ABCD所在平面,M,N分別是AB,PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com