
分析 (1)利用基本不等式的性質(zhì)即可得出.
(2)令ab=x∈$(0,\frac{1}{4}]$.f(x)=x+$\frac{1}{x}$,利用導(dǎo)數(shù)研究其單調(diào)性即可得出.
解答 解:(1)∵正數(shù)a,b滿足a+b=1,∴1$≥2\sqrt{ab}$,解得ab$≤\frac{1}{4}$,當(dāng)且僅當(dāng)a=b=$\frac{1}{2}$時取等號,
∴ab∈$(0,\frac{1}{4}]$.
(2)令ab=x∈$(0,\frac{1}{4}]$.f(x)=x+$\frac{1}{x}$,f′(x)=1-$\frac{1}{{x}^{2}}$<0,因此函數(shù)f(x)在x∈$(0,\frac{1}{4}]$單調(diào)遞減,
∴f(x)≥$f(\frac{1}{4})$=$\frac{17}{4}$.
∴當(dāng)且僅當(dāng)ab=$\frac{1}{4}$時,ab+$\frac{1}{ab}$取得最小值$\frac{17}{4}$.
點評 本題考查了基本不等式的性質(zhì)、利用導(dǎo)數(shù)研究其單調(diào)性極值與最值,考查了推理能力與計算能力,屬于中檔題.


科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (1+ln2,3] | B. | (ln2,3] | C. | (0,1+ln2) | D. | (0,3] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016-2017學(xué)年安徽六安一中高一上國慶作業(yè)二數(shù)學(xué)試卷(解析版) 題型:選擇題
設(shè)函數(shù) ,
, 是
是 上的常數(shù),若
上的常數(shù),若 的值域為
的值域為 ,則
,則 取值范圍為( )
取值范圍為( )
A.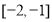 B.
B.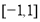
C.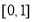 D.
D.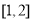
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 重合 | B. | 形狀相同,位置不同 | ||
| C. | 關(guān)于y軸對稱 | D. | 形狀不同,位置不同 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2+2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com