Question

【題目】已知正項(xiàng)數(shù)列的前n項(xiàng)和為，數(shù)列滿足.

（1）求數(shù)列的通項(xiàng)公式；

（2）數(shù)列滿足，它的前n項(xiàng)和為，若存在正整數(shù)n，使不等式成立，求實(shí)數(shù)的取值范圍.

Answer 1

【答案】（1），；（2）或

【解析】

（1）由題意可得當(dāng)時(shí)，，從而推出，則，從而可求出；

（2）易知，利用錯(cuò)位相減法求得，從而有不等式成立，對分奇偶數(shù)討論，令，利用換元法化為二次函數(shù)，從而可求出答案．

解：（1），

當(dāng)時(shí)，，或（舍去）

當(dāng)時(shí)，由，得，

兩式相減得：，，

即，∴．

又∵數(shù)列為正項(xiàng)數(shù)列，故，也即，

∴數(shù)列為以1為首項(xiàng)1為公差的等差數(shù)列，

∴，；

（2）易知，則

①，

②，

①②可得：，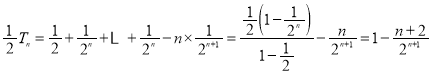

故，所以不等式成立，

若n為偶數(shù)，則，所以，

設(shè)，則在單調(diào)遞減，

故當(dāng)時(shí)，，所以；

若n為奇數(shù)，則，所以

設(shè)，則在單調(diào)遞增，

故當(dāng)時(shí)，，所以，

綜上所述，的取值范圍或.