
| A. | 3 | B. | 4 | C. | 16 | D. | $\frac{1}{256}$ |
分析 運用賦值法,可得f(2)=4,f(3)=8,再由互為反函數的函數圖象關于直線y=x對稱,點(m,n)的對稱點為(n.m),即可得到所求g(8).
解答 解:函數y=f(x)滿足對任意的x,y∈R,都有f(x+y)=f(x)•f(y),且f(1)=2,
可得f(2)=f(1)•f(1)=4,
令x=1,y=2,可得f(3)=f(1)•f(2)=2×4=8,
由g(x)是f(x)的反函數,
可得互為反函數的函數圖象關于直線y=x對稱,
(3,8)關于直線y=x對稱的點為(8,3),
則g(8)=3.
故選:A.
點評 本題考查抽象函數及應用:求函數值,注意運用賦值法,考查互為反函數的函數圖象關于直線y=x對稱,點(m,n)的對稱點為(n.m),考查化簡運算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分又不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,曲線Γ由曲線C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0,y≤0)和曲線C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0,y>0)組成,其中點F1,
如圖,曲線Γ由曲線C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0,y≤0)和曲線C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0,y>0)組成,其中點F1,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
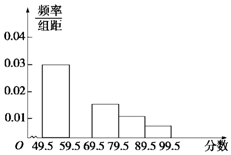 在長豐中學舉行的電腦知識競賽中,將九年級兩個班參賽的學生成績(得分均為整數)進行整理后分成五組,繪制如圖所示的頻率分布直方圖.已知圖中從左到右的第一、第三、第四、第五小組的頻率分別是0.30,0.15,0.10,0.05,第二小組的頻數是40.
在長豐中學舉行的電腦知識競賽中,將九年級兩個班參賽的學生成績(得分均為整數)進行整理后分成五組,繪制如圖所示的頻率分布直方圖.已知圖中從左到右的第一、第三、第四、第五小組的頻率分別是0.30,0.15,0.10,0.05,第二小組的頻數是40.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com