
【題目】母線長為![]() ,底面半徑為
,底面半徑為![]() 的圓錐內有一球
的圓錐內有一球![]() ,與圓錐的側面、底面都相切,現放入一些小球,小球與圓錐底面、側面、球
,與圓錐的側面、底面都相切,現放入一些小球,小球與圓錐底面、側面、球![]() 都相切,這樣的小球最多可放入__________個.
都相切,這樣的小球最多可放入__________個.
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,定義![]() 為兩點
為兩點![]() 、
、
![]() 的“切比雪夫距離”,又設點
的“切比雪夫距離”,又設點![]() 及
及![]() 上任意一點
上任意一點![]() ,稱
,稱![]() 的最小值為點
的最小值為點![]() 到
到
直線![]() 的“切比雪夫距離”,記作
的“切比雪夫距離”,記作![]() ,給出下列三個命題:
,給出下列三個命題:
① 對任意三點![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
② 已知點![]() 和直線
和直線![]() ,則
,則![]() ;
;
③ 定點![]() 、
、![]() ,動點
,動點![]() 滿足
滿足![]() (
(![]() ),
),
則點![]() 的軌跡與直線
的軌跡與直線![]() (
(![]() 為常數)有且僅有2個公共點;
為常數)有且僅有2個公共點;
其中真命題的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過點![]() ,且與圓
,且與圓![]() 外切于點
外切于點![]() ,過點
,過點![]() 作圓C的兩條切線PM,PN,切點為M,N.
作圓C的兩條切線PM,PN,切點為M,N.
(1)求圓C的標準方程;
(2)試問直線MN是否恒過定點?若過定點,請求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() ,
, ![]() ,
, ![]() .給出以下三個命題:
.給出以下三個命題:
①分別過點![]() ,
, ![]() ,作
,作![]() 的不同于
的不同于![]() 軸的切線,兩切線相交于點
軸的切線,兩切線相交于點![]() ,則點
,則點![]() 的軌跡為橢圓的一部分;
的軌跡為橢圓的一部分;
②若![]() ,
, ![]() 相切于點
相切于點![]() ,則點
,則點![]() 的軌跡恒在定圓上;
的軌跡恒在定圓上;
③若![]() ,
, ![]() 相離,且
相離,且![]() ,則與
,則與![]() ,
, ![]() 都外切的圓的圓心在定橢圓上.
都外切的圓的圓心在定橢圓上.
則以上命題正確的是( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,直線
,直線![]() 與雙曲線交于
與雙曲線交于![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)若點![]() 的軌跡與矩形
的軌跡與矩形![]() 的四條邊都相切,探究矩形
的四條邊都相切,探究矩形![]() 對角線長是否為定值,若是,求出此值;若不是,說明理由.
對角線長是否為定值,若是,求出此值;若不是,說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,下有七張卡片,現這樣組成一個三位數:甲從這七張卡片中隨機抽出一張,把卡片上的數字寫在百位,然后把卡片放回;乙再從這七張卡片中隨機抽出一張,把卡片上的數字寫在十位,然后把卡片放回;丙又從這七張卡片中隨機抽出一張,把卡片上的數字寫在個位,然后把卡片放回。則這樣組成的三位數的個數為( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“共享單車”的出現,為我們提供了一種新型的交通方式。某機構為了調查人們對此種交通方式的滿意度,從交通擁堵不嚴重的A城市和交通擁堵嚴重的B城市分別隨機調查了20個用戶,得到了一個用戶滿意度評分的樣本,并繪制出莖葉圖如圖:

(1)根據莖葉圖,比較兩城市滿意度評分的平均值的大小及方差的大小(不要求計算出具體值,給出結論即可);
(2)若得分不低于80分,則認為該用戶對此種交通方式“認可”,否則認為該用戶對此種交通方式“不認可”,請根據此樣本完成此2×2列聯表,并據此樣本分析是否有95%的把握認為城市擁堵與認可共享單車有關;
A | B | 合計 | |
認可 | |||
不認可 | |||
合計 |
(3)在A,B城市對此種交通方式“認可”的用戶中按照分層抽樣的方法抽取6人,若在此6人中推薦2人參加“單車維護”志愿活動,求A城市中至少有1人的概率。
參考數據如下:(下面臨界值表供參考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某種植物每日平均增長高度![]() (單位:
(單位:![]() )與每日光照時間
)與每日光照時間![]() (單位:
(單位:![]() )之間的關系有如下一組數據:
)之間的關系有如下一組數據:
| 6 | 7 | 8 | 9 | 10 |
| 3.5 | 5.2 | 7 | 8.6 | 10.7 |
(1)求![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(2)計算相關指數![]() 的值,并說明回歸模型擬合程度的好壞;
的值,并說明回歸模型擬合程度的好壞;
(3)若某天光照時間為8.5小時, 預測該天這種植物的平均增長高度(結果精確到0.1)
參考公式及數據: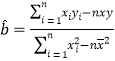 ,
,![]() ,
,![]() ,
,![]()
![]() ,
,,
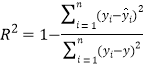
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com