
分析 (Ⅰ)求出函數的導數,通過討論a的范圍,求出函數的單調區間即可;
(Ⅱ)令F(x)=f(x)+(a+1)x+1-e,求出函數的導數,通過討論a的范圍,求出函數的單調區間,從而求出函數F(x)的最大值,進而確定a的范圍即可;
(Ⅲ)令a=1則f(x)=lnx-x,根據函數的單調性得到lnx<x,對x取值,累加即可.
解答 解:(Ⅰ)${f^'}(x)=\frac{a}{x}-a=a(\frac{1}{x}-1)=a\frac{(1-x)}{x}$
當a>0時,f(x)的單調增區間為(0,1],單調減區間為[1,+∞);
當a<0時,f(x)的單調增區間為[1,+∞),單調減區間為(0,1];
(Ⅱ)令F(x)=f(x)+(a+1)x+1-e=alnx+x+1-e
F′(x)=$\frac{x+a}{x}$=0,若-a≤e,a≥-e,F(x) 在[e,e2]是增函數,
$F{(x)_{max}}=F({e^2})=2a+{e^2}-e+1≤0,a≤\frac{{e-1-{e^2}}}{2}$無解.
若e<-a≤e2,-e2≤a<-e,F(x)在[e,-a]是減函數;x∈[-a,e2]是增函數,
F(e)=a+1≤0,a≤-1,.$F({e^2})=2a+{e^2}-e+1≤0,a≤\frac{{e-1-{e^2}}}{2}$
∴-e2≤a≤$\frac{e-1{-e}^{2}}{2}$,若-a>e2,a<-e2,F(x)x∈[e,e2]是減函數,
F(x)max=F(e)=a+1≤0,a≤-1,∴a<-e2,
綜上所述a≤$\frac{e-1{-e}^{2}}{2}$ (或用參數分離法)
(Ⅲ)令a=1則f(x)=lnx-x
由(1)知f(x)在[1,+∞)上單調遞減,又因為
f(1)<0,所以有lnx<x,
即ln2<2,ln3<3…lnn<n,
∴$lnn!≤\frac{(n+2)(n-1)}{2}$.
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及不等式的證明,是一道中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{4}{5}$ | C. | -1 | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
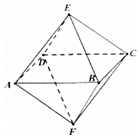
| A. | 不平行的兩條棱所在的直線所成的角是60o或90o | |
| B. | 四邊形AECF是正方形 | |
| C. | 點A到平面BCE的距離為$\frac{\sqrt{6}}{3}$ | |
| D. | 該八面體的頂點不會在同一個球面上. |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | d<0 | B. | a7=0 | ||
| C. | S${\;}_{{9}_{\;}}$>S5 | D. | S6和S7均為Sn的最大值 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com