
| A. | $f(x)=sin(\frac{π}{3}x)$ | B. | $f(x)=sin(\frac{π}{2}x)$ | C. | $f(x)=cos(\frac{π}{3}x)$ | D. | $f(x)=cos(\frac{π}{2}x)$ |
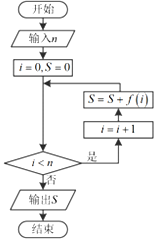
分析 模擬程序的運行,可得程序框圖的功能是計算并輸出S=f(1)+f(2)+…+f(2017)的值,由S=f(1)+f(2)+…+f(2017)=0,觀察四個選項,利用正弦函數,余弦函數值的周期性即可計算得解.
解答 解:模擬程序的運行,可得程序框圖的功能是計算并輸出S=f(1)+f(2)+…+f(2017)的值,
由于S=f(1)+f(2)+…+f(2017)=0,
觀察四個選項,相位為$\frac{π}{3}x$的三角函數的最小正周期為$\frac{2π}{{\frac{π}{3}}}=6$,
對于選項A:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=336(f(1)+f(2)+…++f(6))+f(2017)\\=f(2017)=f(1)=sin\frac{π}{3}≠0\end{array}$
故排除;
選項C:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=336(f(1)+f(2)+…++f(6))+f(2017)\\=f(2017)=f(1)=cos\frac{π}{3}≠0\end{array}$
故排除;
由于,相位為$\frac{π}{2}x$的三角函數的最小正周期為$\frac{2π}{{\frac{π}{2}}}=4$,
選項B:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=504(f(1)+f(2)+…++f(4))+f(2017)\\=f(2017)=f(1)=sin\frac{π}{2}≠0\end{array}$,
故排除.
選項D:
$\begin{array}{l}S=f(1)+f(2)+…+f(2017)=504(f(1)+f(2)+…++f(4))+f(2017)\\=f(2017)=f(1)=cos\frac{π}{2}=0\end{array}$
故正確.
故選:D.
點評 本題主要考查了循環結構的程序框圖的應用,考查了正弦函數,余弦函數的周期性,模擬程序的運行得程序框圖的功能是解題的關鍵,屬于基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{1}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com