Question

6．若圓C：x²+y²-2x+4y-20=0上有四個不同的點到直線l：4x+3y+c=0的距離為2，則c的取值范圍是（　　）

• A． （-12，8）
• B． （-8，12）
• C． （-13，17）
• D． （-17，13）

Answer 1

分析 由題意畫出圖形，若圓C：（x-1）²+（y+2）²=25有四個不同的點到直線l：4x+3y+c=0的距離為2，則圓心C（1，-2）到直線l的距離d＜3，由此列關于c的不等式得答案．

解答 解：圓C：x²+y²-2x+4y-20=0化為（x-1）²+（y+2）²=25，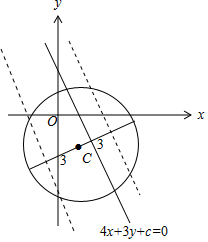
則圓心C為（1，-2），半徑r=5．
若圓C：（x-1）²+（y+2）²=25有四個不同的點到直線l：4x+3y+c=0的距離為2，
則圓心C（1，-2）到直線l的距離d＜3，
如圖：
即$\frac{|4×1+3×（-2）+c|}{5}$=$\frac{|c-2|}{5}$＜3，解得：-13＜c＜17，
∴c的取值范圍是（-13，17）．
故選：C．

點評 本題考查直線與圓的位置關系，考查點到直線距離公式的應用，體現了數形結合的解題思想方法，是中檔題．