
分析 (1)求導函數,求出函數的零點,再進行分類討論,從而可確定函數y=f(x)的單調性與單調區間.
(2)f(x)有極大值與極小值,由(1)可知,0<a<2或a>2,根據函數零點定理驗證即可.
解答 解:(1)由題意得,f′(x)=2x-(a+2)+$\frac{a}{x}$=$\frac{(x-1)(2x-a)}{x}$(x>0),
由f′(x)=0,得x1=1,x2=$\frac{a}{2}$
①當0<$\frac{a}{2}$<1,即0<a<2,令f′(x)>0,又x>0,可得0<x<$\frac{a}{2}$或x>1;
令f′(x)<0,x>0,可得$\frac{a}{2}$<x<1,
∴函數f(x)的單調增區間是(0,$\frac{a}{2}$)和(1,+∞),單調減區間是($\frac{a}{2}$,1);
②當$\frac{a}{2}$=1,即a=2時,f′(x)=$\frac{2(x-1)^{2}}{x}$≥0,當且僅當x=1時,f′(x)=0,
∴函數f(x)在區間(0,+∞)上是單調增函數;
③當$\frac{a}{2}$>1,即a≥2時,令f′(x)>0,又x>0,可得0<x<1或x>$\frac{a}{2}$;
令f′(x)<0,x>0,可得1<x<$\frac{a}{2}$
∴函數f(x)的單調增區間是(0,1)和($\frac{a}{2}$,+∞),單調減區間是(1,$\frac{a}{2}$);
④當$\frac{a}{2}$≤0,即a≤0時,令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)遞減,在(1,+∞)遞增.
(2)∵f(x)有極大值與極小值,由(1)可知,0<a<2或a>2,
當a>2時,函數f(x)的單調增區間是(0,1)和($\frac{a}{2}$,+∞),單調減區間是(1,$\frac{a}{2}$),
若x∈(0,$\frac{a}{2}$),f(x)≤f(1)=-a-1<0,無零點,
若x∈($\frac{a}{2}$,+∞),則f($\frac{a}{2}$)<f(1)<0,
f(a+2)=aln(a+2)>0,有一個零點,
則當a>2時,f(x)有唯一的零點,
當0<a<2函數f(x)的單調增區間是(0,$\frac{a}{2}$)和(1,+∞),單調減區間是($\frac{a}{2}$,1);
若x∈(0,1),f(x)≤f($\frac{a}{2}$)=a(lna-$\frac{a}{4}$-1-ln2),
有lna<ln2<1,則lna-$\frac{a}{4}$-1-ln2<0,則f(x)<0,即f(x)在(0,1)內無零點,
若x∈(1,+∞),則<f(1)<0,f(a+2)=aln(a+2)>0,即f(x)在[1,+∞)有一個零點,
則當0<a<2時,f(x)有唯一的零點,
綜上所述函數f(x)在定義域內有唯一的零點
點評 本題重點考查導數知識的運用和函數零點定理,考查函數的單調性,利用導數的正負確定函數的單調性是關鍵,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
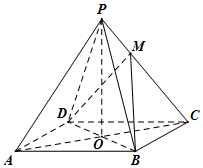 如圖,已知四棱錐P-ABCD的底面是菱形,對角線AC,BD交于點O,OA=4,OB=3,OP=4,OP⊥底面ABCD,設點M滿足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).
如圖,已知四棱錐P-ABCD的底面是菱形,對角線AC,BD交于點O,OA=4,OB=3,OP=4,OP⊥底面ABCD,設點M滿足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
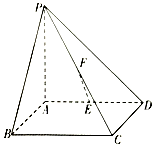 如圖,四棱錐P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分別為AD,PC的中點.
如圖,四棱錐P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分別為AD,PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com