
 雙曲線C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦點分別為F1,F(xiàn)2,過F2作x軸垂直的直線交雙曲線C于A、B兩點,△F1AB的面積為12,拋物線E:y2=2px(p>0)以雙曲線C的右頂點為焦點.
雙曲線C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦點分別為F1,F(xiàn)2,過F2作x軸垂直的直線交雙曲線C于A、B兩點,△F1AB的面積為12,拋物線E:y2=2px(p>0)以雙曲線C的右頂點為焦點.分析 (Ⅰ)設F2(c,0),由令x=c代入C的方程有:$|{y_A}|=\frac{3}{a}$,求出A的縱坐標,代入三角形面積公式求得c,則拋物線方程可求;
(Ⅱ)由(Ⅰ)可得M坐標,寫出直線PO的方程,與拋物線方程聯(lián)立可得N的坐標,當t2≠4時,寫出MN所在直線方程,化簡后說明直線MN過定點(1,0),當t2=4時,直線MN的方稱為:x=1,此時仍過點(1,0).
解答 (Ⅰ)解:設F2(c,0)(c>0),則$c=\sqrt{{a^2}+3}$
令x=c代入C的方程有:$|{y_A}|=\frac{3}{a}$
∴${S_{△{F_1}AB}}=\frac{1}{2}×2c×2|{y_A}|=\frac{{6\sqrt{{a^2}+3}}}{a}=12$
∴a=1,故$\frac{p}{2}=a=1$,即p=2
∴拋物線E的方稱為:y2=4x
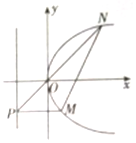
(Ⅱ)證明:由(Ⅰ)知:P(-1,t)(t≠0),則$M({\frac{t^2}{4},t})$
直線PO的方稱為y=-tx,代入拋物線E的方程有:$N({\frac{4}{t^2},-\frac{4}{t}})$
當t2≠4時,${k_{MN}}=\frac{{t+\frac{4}{t}}}{{\frac{t^2}{4}-\frac{4}{t^2}}}=\frac{4t}{{{t^2}-4}}$
∴直線MN的方程為:$y-t=\frac{4t}{{{t^2}-4}}({x-\frac{t^2}{4}})$,即$y=\frac{4t}{{{t^2}-4}}({x-1})$
∴此時直線MN過定點(1,0)
當t2=4時,直線MN的方稱為:x=1,此時仍過點(1,0)
即證直線MN過定點
點評 本題考查雙曲線與拋物線的簡單性質,考查了雙曲線與拋物線關系的應用,體現(xiàn)了分類討論的數(shù)學思想方法,是中檔題.


科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{\sqrt{10}}{4}$ | B. | $\frac{10+\sqrt{10}}{5}$ | C. | $\frac{10-\sqrt{10}}{5}$ | D. | $\frac{10+2\sqrt{10}}{5}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | [3,8] | B. | (3,8) | C. | [3,13] | D. | (3,13) |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com