
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | c>b>a |
分析 ∴對任意兩個不等的正實數x1,x2,都有$\frac{{x}_{1}{x}_{2}(\frac{1}{{x}_{1}}f({x}_{1})-\frac{1}{{x}_{2}}f({x}_{2}))}{{x}_{1}-{x}_{2}}<0$⇒$\frac{\frac{1}{{x}_{1}}f({x}_{1})-\frac{1}{{x}_{2}}f({x}_{2})}{{x}_{1}-{x}_{2}}<0$,令g(x)=$\frac{1}{x}f(x)$,易得g(x)在(0,+∞)上遞減即可.
解答 解:定義域為R的函數f(x)滿足:對任意兩個不等的實數x1,x2,都有$\frac{{{x_2}f({x_1})-{x_1}f({x_2})}}{{{x_1}-{x_2}}}<0$,
∴對任意兩個不等的正實數x1,x2,都有$\frac{{x}_{1}{x}_{2}(\frac{1}{{x}_{1}}f({x}_{1})-\frac{1}{{x}_{2}}f({x}_{2}))}{{x}_{1}-{x}_{2}}<0$⇒$\frac{\frac{1}{{x}_{1}}f({x}_{1})-\frac{1}{{x}_{2}}f({x}_{2})}{{x}_{1}-{x}_{2}}<0$,
令g(x)=$\frac{1}{x}f(x)$,易得g(x)在(0,+∞)上遞減,a=4f(0.25)=g(0.25),b=0.5f(2)=g(2),c=0.2f(5)=g(5),
∴g(0.25)>g(2)>g(5),⇒a>b>c.故選:A.
點評 本題考查了構造新函數,函數的單調性的運用,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | ②、③ | B. | ③、④ | C. | ①、④ | D. | ①、② |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
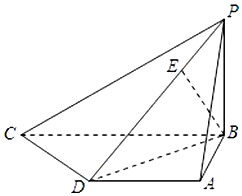 已知四棱錐P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,點E在棱PD上,且BE⊥PD.
已知四棱錐P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,點E在棱PD上,且BE⊥PD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
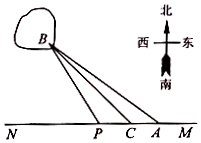 如圖,已知A,B兩鎮分別位于東西湖岸MN的A處和湖中小島的B處,點C在A的正西方向1km處,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,現計劃鋪設一條電纜聯通A,B兩鎮,有兩種鋪設方案:①沿線段AB在水下鋪設;②在湖岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設,預算地下、水下的電纜鋪設費用分別為2萬元∕km、4萬元∕km.
如圖,已知A,B兩鎮分別位于東西湖岸MN的A處和湖中小島的B處,點C在A的正西方向1km處,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,現計劃鋪設一條電纜聯通A,B兩鎮,有兩種鋪設方案:①沿線段AB在水下鋪設;②在湖岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設,預算地下、水下的電纜鋪設費用分別為2萬元∕km、4萬元∕km.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
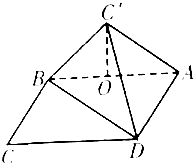 如圖.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿對角線BD把△BCD折起.使C移到C′.且C′在面ABC內的射影O恰好落在AB上.
如圖.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿對角線BD把△BCD折起.使C移到C′.且C′在面ABC內的射影O恰好落在AB上.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1} | B. | (0,1] | C. | [1,+∞) | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com