
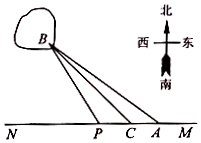
 如圖,已知A,B兩鎮分別位于東西湖岸MN的A處和湖中小島的B處,點C在A的正西方向1km處,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,現計劃鋪設一條電纜聯通A,B兩鎮,有兩種鋪設方案:①沿線段AB在水下鋪設;②在湖岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設,預算地下、水下的電纜鋪設費用分別為2萬元∕km、4萬元∕km.
如圖,已知A,B兩鎮分別位于東西湖岸MN的A處和湖中小島的B處,點C在A的正西方向1km處,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,現計劃鋪設一條電纜聯通A,B兩鎮,有兩種鋪設方案:①沿線段AB在水下鋪設;②在湖岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設,預算地下、水下的電纜鋪設費用分別為2萬元∕km、4萬元∕km.分析 (1)由tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,得到|AD|,|DB|、|AB|間的關系,然后利用直角三角形的性質求解;
(2)方案①:總鋪設費用為5×4=20(萬元).
方案②:設∠BPD=θ,則$θ∈({θ_0},\frac{π}{2})$,其中θ0=∠BAN,
在Rt△BDP中,$DP=\frac{BD}{tanθ}=\frac{3}{tanθ}$,$BP=\frac{BD}{sinθ}=\frac{3}{sinθ}$,
則總鋪設費用為$2AP+4BP=8-\frac{6}{tanθ}+\frac{12}{sinθ}=8+6•\frac{2-cosθ}{sinθ}$.
設$f(θ)=\frac{2-cosθ}{sinθ}$,則$f'(θ)=\frac{{{{sin}^2}θ-(2-cosθ)cosθ}}{{{{sin}^2}θ}}=\frac{1-2cosθ}{{{{sin}^2}θ}}$,
,求出函數的極小值,即函數的最小值得答案.
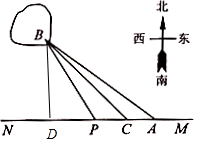
解答 解:(1)過B作MN的垂線,垂足為D,如圖示:
在Rt△ABD中,$tan∠BAD=tan∠BAN=\frac{BD}{AD}=\frac{3}{4}$,
所以$AD=\frac{4}{3}BD$,
在Rt△BCD中,$tan∠BCD=tan∠BCN=\frac{BD}{CD}=1$,
所以CD=BD.
則$AC=AD-CD=\frac{4}{3}BD-BD=\frac{1}{3}BD=1$,即BD=3,
所以CD=3,AD=4,
由勾股定理得,$AB=\sqrt{A{D^2}+B{D^2}}=5$(km).
所以A,B兩鎮間的距離為5km.…(4分)
(2)方案①:沿線段AB在水下鋪設時,總鋪設費用為5×4=20(萬元).…(6分)
方案②:設∠BPD=θ,則$θ∈({θ_0},\frac{π}{2})$,其中θ0=∠BAN,
在Rt△BDP中,$DP=\frac{BD}{tanθ}=\frac{3}{tanθ}$,$BP=\frac{BD}{sinθ}=\frac{3}{sinθ}$,
所以$AP=4-DP=4-\frac{3}{tanθ}$.
則總鋪設費用為$2AP+4BP=8-\frac{6}{tanθ}+\frac{12}{sinθ}=8+6•\frac{2-cosθ}{sinθ}$.…(8分)
設$f(θ)=\frac{2-cosθ}{sinθ}$,則$f'(θ)=\frac{{{{sin}^2}θ-(2-cosθ)cosθ}}{{{{sin}^2}θ}}=\frac{1-2cosθ}{{{{sin}^2}θ}}$,
令f'(θ)=0,得$θ=\frac{π}{3}$,列表如下:
| θ | $({θ_0},\frac{π}{3})$ | $\frac{π}{3}$ | $(\frac{π}{3},\frac{π}{2})$ |
| f'(θ) | - | 0 | + |
| f(θ) | ↘ | 極小值 | ↗ |
點評 本題考查了簡單的數學建模思想方法,考查了利用導數求函數的最值,是中檔題


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
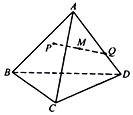 如圖,在三棱錐A-BCD中,AB⊥AD,AC⊥AD,∠BAC=60°,AB=AC=AD=4,點P,Q分別在側面ABC棱AD上運動,PQ=2,M為線段PQ中點,當P,Q運動時,點M的軌跡把三棱錐A-BCD分成上、下兩部分的體積之比等于$\frac{π}{{48\sqrt{3}-π}}$.
如圖,在三棱錐A-BCD中,AB⊥AD,AC⊥AD,∠BAC=60°,AB=AC=AD=4,點P,Q分別在側面ABC棱AD上運動,PQ=2,M為線段PQ中點,當P,Q運動時,點M的軌跡把三棱錐A-BCD分成上、下兩部分的體積之比等于$\frac{π}{{48\sqrt{3}-π}}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,2] | B. | [$\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,1] | D. | (-∞,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [6-2$\sqrt{6}$,9] | B. | [6-2$\sqrt{6}$,11] | C. | [6+2$\sqrt{6}$,9] | D. | [6+2$\sqrt{6}$,11] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com