
分析 由${S_{n+1}}=\frac{2}{3}{a_{n+1}}+\frac{1}{3}$(n∈z+),可推出Sn=$\frac{2}{3}$an+$\frac{1}{3}$,從而可得{an}是以-5為首項,-2為公比的等比數列,從而解出數列的通項公式.
解答 解:∵${S_{n+1}}=\frac{2}{3}{a_{n+1}}+\frac{1}{3}$(n∈z+),可推出Sn=$\frac{2}{3}$an+$\frac{1}{3}$,n≥2,兩式作差的,an+1=$\frac{2}{3}$an+1-$\frac{2}{3}$an,
即an+1=-2an,
則{an}是以a2為首項,-2為公比的等比數列,數列{an}的首項a1=2,∴a1+a2=$\frac{2}{3}$a2+$\frac{1}{3}$,
a2=-5,
則an=-5•(-2)n-2.n≥2.
數列的通項公式為:${a_n}=\left\{\begin{array}{l}2,n=1\\-5{(-2)^{n-2}},n≥2\end{array}\right.$.
故答案為:$\left\{\begin{array}{l}{2,n=1}\\{-5•(-2)^{n-2},n≥2}\end{array}\right.$.
點評 本題考查了數列的通項公式的推導,數列遞推關系式的應用,考查計算能力.


科目:高中數學 來源: 題型:選擇題
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -sin3-cos3 | B. | sin3-cos3 | C. | sin3+cos3 | D. | cos3-sin3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $sin\sqrt{2}<cos\sqrt{2}<tan\sqrt{2}$ | B. | $cos\sqrt{2}<sin\sqrt{2}<tan\sqrt{2}$ | C. | $cos\sqrt{2}<tan\sqrt{2}<sin\sqrt{2}$ | D. | $sin\sqrt{2}<tan\sqrt{2}<cos\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
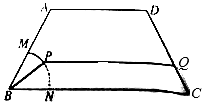 如圖,某公園中間有一塊等腰梯形的綠化區ABCD,AB,CD的長度相等,均為2百米,BC的長度為4百米,其中BMN是半徑為1百米的扇形,$∠ABC=\frac{π}{3}$.管理部門欲在綠化區ABCD中修建從M到C的觀賞小路$\widehat{MP}-PQ-QC$;其中P為$\widehat{MN}$上異于M,N的一點,小路PQ與BC平行,設∠PBC=θ.
如圖,某公園中間有一塊等腰梯形的綠化區ABCD,AB,CD的長度相等,均為2百米,BC的長度為4百米,其中BMN是半徑為1百米的扇形,$∠ABC=\frac{π}{3}$.管理部門欲在綠化區ABCD中修建從M到C的觀賞小路$\widehat{MP}-PQ-QC$;其中P為$\widehat{MN}$上異于M,N的一點,小路PQ與BC平行,設∠PBC=θ.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com