
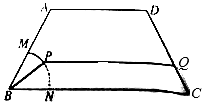
 如圖,某公園中間有一塊等腰梯形的綠化區ABCD,AB,CD的長度相等,均為2百米,BC的長度為4百米,其中BMN是半徑為1百米的扇形,$∠ABC=\frac{π}{3}$.管理部門欲在綠化區ABCD中修建從M到C的觀賞小路$\widehat{MP}-PQ-QC$;其中P為$\widehat{MN}$上異于M,N的一點,小路PQ與BC平行,設∠PBC=θ.
如圖,某公園中間有一塊等腰梯形的綠化區ABCD,AB,CD的長度相等,均為2百米,BC的長度為4百米,其中BMN是半徑為1百米的扇形,$∠ABC=\frac{π}{3}$.管理部門欲在綠化區ABCD中修建從M到C的觀賞小路$\widehat{MP}-PQ-QC$;其中P為$\widehat{MN}$上異于M,N的一點,小路PQ與BC平行,設∠PBC=θ.分析 (1)過P作PP1⊥BC于P1,過Q作QQ1⊥BC于Q1,先計算BN,PP1,再得出CQ1即可得出PQ的長;
(2)求出觀賞小路長度關于θ的函數f(θ),利用導數求出f(θ)的單調性,總而得出觀賞小路最小時對應的θ值.
解答 解:(1)過P作PP1⊥BC于P1,過Q作QQ1⊥BC于Q1,
∵∠PBC=θ,BP=1,
∴QQ1=PP1=sinθ,BP1=cosθ,
在Rt△QCQ1中,tan∠QCQ1=$\frac{Q{Q}_{1}}{C{Q}_{1}}$=$\sqrt{3}$,∴CQ1=$\frac{\sqrt{3}}{3}$sinθ,
∴PQ=P1Q1=4-cosθ-$\frac{\sqrt{3}}{3}$sinθ,(0<θ<$\frac{π}{3}$),
(2)在Rt△QCQ1中,sin∠QCQ1=$\frac{Q{Q}_{1}}{CQ}$=$\frac{\sqrt{3}}{2}$,∴CQ=$\frac{2\sqrt{3}}{3}$sinθ,
∵∠PBC=θ,∠ABC=$\frac{π}{3}$,BP=1,
∴$\widehat{MP}$=$\frac{π}{3}$-θ,
設觀賞小路的總長度為f(θ),則f(θ)=$\frac{π}{3}$-θ+4-cosθ-$\frac{\sqrt{3}}{3}$sinθ+$\frac{2\sqrt{3}}{3}$sinθ=$\frac{π}{3}$-θ+4-cosθ+$\frac{\sqrt{3}}{3}$sinθ(0<θ<$\frac{π}{3}$),
∴f′(θ)=sinθ+$\frac{\sqrt{3}}{3}$cosθ-1=$\frac{2\sqrt{3}}{3}$sin($θ+\frac{π}{6}$)-1,
令f′(θ)=0得sin($θ+\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,解得θ=$\frac{π}{6}$,
當0<θ<$\frac{π}{6}$時,f′(θ)<0,當$\frac{π}{6}$<θ<$\frac{π}{3}$時,f′(θ)>0,
∴f(θ)在(0,$\frac{π}{6}$)上單調遞減,在($\frac{π}{6}$,$\frac{π}{3}$)上單調遞增,
∴當θ=$\frac{π}{6}$時,f(θ)取得最小值,
∴當θ=$\frac{π}{6}$時,觀賞小路$\widehat{MP}-PQ-QC$的總長度最短.
點評 本題考查了函數解析式的求解,導數與函數最值的關系,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖所示,一個圓柱形乒乓球筒,高為20厘米,底面半徑為2厘米.球筒的上底和下底分別粘有一個乒乓球,乒乓球與球筒底面及側面均相切(球筒和乒乓球厚度均忽略不計).一個平面與兩個乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個橢圓,則該橢圓的離心率為$\frac{\sqrt{15}}{4}$.
如圖所示,一個圓柱形乒乓球筒,高為20厘米,底面半徑為2厘米.球筒的上底和下底分別粘有一個乒乓球,乒乓球與球筒底面及側面均相切(球筒和乒乓球厚度均忽略不計).一個平面與兩個乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個橢圓,則該橢圓的離心率為$\frac{\sqrt{15}}{4}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com