
分析 (1)根據等比數列的通項公式即可求得公式比q,2a1+3a1q=1,則a1=$\frac{1}{3}$.根據等比數列的通項公式即可求得{bn}的通項公式;
(2)$\frac{1}{{b}_{n}}$=-$\frac{2}{n(n+1)}$=-2($\frac{1}{n}$-$\frac{1}{n+1}$),累加即可求得數列{$\frac{1}{{b}_{n}}$}的前n項和,利用等比數列前n項和公式求得數列{an}前n項和,相加即可求得數列{cn}的前n項和Sn.
解答 解:(1)設數列{an}的公比為q,由a32=9a2a6得a32=9a42,則q2=$\frac{1}{9}$,由條件可知各項均為正數,故q=$\frac{1}{3}$.
由2a1+3a2=1,得2a1+3a1q=1,
∴a1=$\frac{1}{3}$.故數列{an}的通項式為an=$\frac{1}{{3}^{n}}$.
bn=log3a1+log3a2+…+log3an=-(1+2+…+n)=-$\frac{n(n+1)}{2}$,
∴數列{an}的通項式為an=-$\frac{n(n+1)}{2}$.
(2)故$\frac{1}{{b}_{n}}$=-$\frac{2}{n(n+1)}$=-2($\frac{1}{n}$-$\frac{1}{n+1}$)則$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$=-2[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)]=-$\frac{2n}{n+1}$,
∴數列{$\frac{1}{{b}_{n}}$}的前n項和為-$\frac{2n}{n+1}$.
等比數列{an}前n項和Tn,Tn=$\frac{\frac{1}{3}-\frac{1}{{3}^{n+1}}}{1-\frac{1}{3}}$=$\frac{1-\frac{1}{{3}^{n}}}{2}$=$\frac{1}{2}$-$\frac{1}{2×{3}^{n}}$,
數列{cn}的前n項和Sn=$\frac{1}{2}$-$\frac{1}{2×{3}^{n}}$-$\frac{2n}{n+1}$.
點評 本題考查等比數列通項公式,等比數列前n項和公式,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
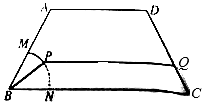 如圖,某公園中間有一塊等腰梯形的綠化區ABCD,AB,CD的長度相等,均為2百米,BC的長度為4百米,其中BMN是半徑為1百米的扇形,$∠ABC=\frac{π}{3}$.管理部門欲在綠化區ABCD中修建從M到C的觀賞小路$\widehat{MP}-PQ-QC$;其中P為$\widehat{MN}$上異于M,N的一點,小路PQ與BC平行,設∠PBC=θ.
如圖,某公園中間有一塊等腰梯形的綠化區ABCD,AB,CD的長度相等,均為2百米,BC的長度為4百米,其中BMN是半徑為1百米的扇形,$∠ABC=\frac{π}{3}$.管理部門欲在綠化區ABCD中修建從M到C的觀賞小路$\widehat{MP}-PQ-QC$;其中P為$\widehat{MN}$上異于M,N的一點,小路PQ與BC平行,設∠PBC=θ.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{3}π$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{12}-\frac{y^2}{24}=1$ | B. | $\frac{y^2}{12}-\frac{x^2}{24}=1$ | C. | $\frac{y^2}{24}-\frac{x^2}{12}=1$ | D. | $\frac{x^2}{24}-\frac{y^2}{12}=1$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com